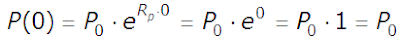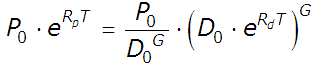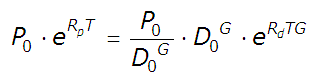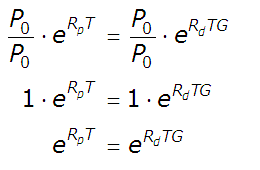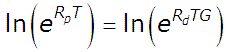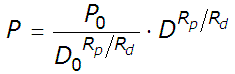Not long ago, we revealed the basic mathematical equation that describes the relationship between share prices and dividends in the stock market, which we found works better than the Price Earnings Ratio (P/E Ratio) as a gage that you may use to assess the valuation of the stock market. The general form of that equation is:

The most important part of this equation is the exponent G, which we stated to be the ratio of the growth rate of stock prices and the growth rate of dividends per share.

Well, we stated that, but we didn't show that. We're going to show how to get there today, but in doing so, we recognize that we risk having a major portion of our audience tune out entirely, as there's nothing more boring than reading a blog post with a lot of math in it. We're well aware that incorporating a lot of math into a blog post can really deliver the kiss of death for reader interest. Unless, that is, there's some other hook to capture the reader's attention.

So, with your as-of-now willing consent, we're going to simultaneously conduct an experiment in mind control. If you don't want to participate, you really need to back out now.

Still here? Good! What enables our ability to seize control of your advanced mental functions is a technology invented back in the 1990s called "hypno-helio-static-stasis." Developed by Dr. Clayton Forrester, hypno-helio-static-stasis breaks down the neural synapses centered in the portion of your brain that controls your free will, rendering you unable to exercise that free will.

The key to the technology hinges upon it being delivered via a medium that would normally simply cause great boredom to descend upon you, which creates the necessary conditions by which certain neural receptors become vulnerable to the control technology, X-4. In his day, Dr. Forrester used the movie "Radar Secret Service" as his primary delivery vehicle. Today, we're going to use math, which should work just as well, if not better. We'll be monitoring your progress as we go along. Let's get started.

We'll begin by noting that both share prices, as represented by the index value of the S&P 500, and dividends per share have historically both exhibited exponential growth over much of their histories, which is confirmed by regression analysis (shown in the two charts below, which provide the average monthly figures for each covering the modern era for dividends in the S&P 500):

The general form of these exponential functions, as taken from an arbitrary starting point in time, t₀, is given by:

Share Price:

Dividends per Share:

where:

P₀ = Share Price at the arbitrary starting point in time
D₀ = Dividends per Share at the starting point in time
R_p = Growth Rate of the Share Price
R_d = Growth Rate of Dividends per Share
t = A subsequent point in Time (occurring after the arbitrary starting point)

For shorthand purposes, we'll rewrite the difference between t and t₀ as: T = t - t₀, which represents Elapsed Time. Rewriting these equations with this shorthand, we get:

Share Price:

Dividends per Share:

From here, we'll substitute these expressions into our equation that defines the relationship between Share Price, P and Dividends per Share, D:

This becomes, after our substitutions:

The next step will be to deal with the constant, A. We'll do this by noting our boundary conditions, which are defined at the arbitrary starting point represented by our equations, when the Elapsed Time is equal to zero:

Initial Share Price:

Initial Dividends per Share:

Making these replacements representing the initial Share Price and Dividends per Share into our equation gives us the following:

We can now solve for A, which turns out to be the ratio of the Share Price and the Dividends per Share raised to the power, G:

All that's now left to determine in our formulation of the relationship between Share Price and Dividends per Share is "G". We'll replace A with the value we just found in our more general equation:

Applying the properties of exponents, namely those of raising a power to a power and raising a product to a power, we can rewrite this equation as follows:

With the term D₀^G appearing in both the numerator and denominator in the expression on the right hand side of our equation, we verify that this portion of our term is equal to one, effectively cancelling it out of the equation:

Our next step will be to eliminate the P₀ term in the equation by dividing both sides of the equation by P₀:

From here, we'll take the natural logarithm of both sides of the equation:

Since the natural logarithm is the inverse of the exponential function, we can now write our equation as:

We can now solve directly for G. Dividing both sides of the equation by R_dT, we obtain our final result:

This result confirms that the exponent G is the ratio of the Growth Rate of Share Price and the Growth Rate of Dividends per Share. For simplicity, we'll call this relationship the Price-Dividend Growth Ratio, or maybe even more simply, the G-Ratio!

We can now write our fundamental stock market equation relating share prices and dividends per share as follows:

And that concludes our experiment, all except for the post-hypno-helio-static-stasis suggestion we implanted and will activate at some arbitrary time in the future. Until then, your free will, such as it is, is now again your own. Thank you for participating!

Labels: math, SP 500

- posted by Ironman at 12:38 PM | Permalink |

|