Mathematics is very unlike any other discipline, and 2017 demonstrated it in spades!
Imagine, if you will, what it takes to prove out a hypothesis or conjecture in science. Years of careful and often costly experimentation or observation produces results that, should any tiny detail lead to results that might overturn part or all of the hypothesis and its predictions through new observations and experiments, will lead to the hypothesis being tested more acutely or perhaps continue to be used after having its limitations considered (the best case scenario), shelved, or unceremoniously dumped into the rubbish bin of failed scientific propositions. Starts With a Bang's Ethan Siegel recently lamented that scientific proof is a myth:
You've heard of our greatest scientific theories: the theory of evolution, the Big Bang theory, the theory of gravity. You've also heard of the concept of a proof, and the claims that certain pieces of evidence prove the validities of these theories. Fossils, genetic inheritance, and DNA prove the theory of evolution. The Hubble expansion of the Universe, the evolution of stars, galaxies, and heavy elements, and the existence of the cosmic microwave background prove the Big Bang theory. And falling objects, GPS clocks, planetary motion, and the deflection of starlight prove the theory of gravity.
Except that's a complete lie. While they provide very strong evidence for those theories, they aren't proof. In fact, when it comes to science, proving anything is an impossibility.
The reason that absolute scientific proof is an impossibility is because reality is, in reality, very complicated. Our limitations as real people living in the real world constrains our ability to see, test or even to imagine every possible detail of existence that might affect how reality works. As a result, every genuine scientific theory and hypothesis can potentially be shown to be false, which is a major part of what separates science from pseudoscience.
There is only one serious human discipline that doesn't have that limitation: mathematics. One of the most fun descriptions that gets into what mathematical proofs can do that scientific proofs cannot that we saw this year was presented in Thomas Oléron Evans and Hannah Fry's book The Indisputable Existence of Santa Claus: The Mathematics of Christmas:
The scientific method takes a theory - in our case that Santa is real - and sets about trying to prove that it is false. Although this may seem a little counterintuitive on the surface, it actually does make a lot of sense. If you go out looking for evidence that Santa doesn't exist and don't find any ... well then, that is pretty revealing. The harder you try, and fail, to show that Santa cannot exist, the more support youy have for your theory that he must. Eventually, when enough evidence has been gathered that all points in the same direction, your original theory is accepted as fact.
Mathematical proof is different. In mathematics, proving something "beyond all reasonable doubt" isn't good enough. You have to prove it beyond all unreasonable doubt as well. Mathematicians aren't happy unless they have demonstrated the truth of a theory absolutely, irrefutably, irrevocably, categorically, indubitably, unequivocally, and indisputably. In mathematics, proof really means proof, and once something is mathematically true, it is true forever. Unlike, say, the theory of gravity - hey, Newton?
So with the differences between the nature of scientific and mathematical proofs in mind, let's get to the biggest math stories of 2017 where, because we're practical people who live in the real world, we've focused upon the stories where the outcome of maths can make a practical difference to people's lives.
Have you ever walked around with an open-topped cup of coffee? If so, you probably have run into the problem of having the contents of your mug slosh and spill out as you attempted to walk with it, which wastes both your precious coffee and, if it gets on your hands, potentially causes burns requiring first aid. Fortunately, 2017 is the year in which mathematics solved the problem of sloshing coffee!
Americans drink an average of 3.1 cups of coffee per day; for many people, the popular beverage is a morning necessity. When carrying a liquid, common sense says to walk slowly and refrain from overfilling the container. But when commuters rush out the door with coffee in hand, chances are their hastiness causes some of the hot liquid to slosh out of the cup. The resulting spills, messes, and mild burns undoubtedly counteract coffee's savory benefits.
Sloshing occurs when a vessel of liquid—coffee in a mug, water in a bucket, liquid natural gas in a tanker, etc.—oscillates horizontally around a fixed position near a resonant frequency; this motion occurs when the containers are carried or moved. While nearly all transport containers have rigid handles, a bucket with a pivoted handle allows rotation around a central axis and greatly reduces the chances of spilling. Although this is not necessarily a realistic on-the-go solution for most beverages, the mitigation or elimination of sloshing is certainly desirable. In a recent article published in SIAM Review, Hilary and John Ockendon use surprisingly simple mathematics to develop a model for sloshing. Their model comprises a mug on a smooth horizontal table that oscillates in a single direction via a spring connection. "We chose the mathematically simplest model with which to understand the basic mechanics of pendulum action on sloshing problems," J. Ockendon said.
But that's not the best part of the story! That part comes from where the idea for the study originated, which illustrates Evans and Fry's point of the extremes to which mathematicians will go that scientists do not:
The authors derive their inspiration from an Ig Nobel prize-winning paper describing a basic mechanical model that investigates the results of walking backwards while carrying a cup of coffee....
The authors evaluate this scenario rather than the more realistic but complicated use of a mug as a cradle that moves like a simple pendulum. To further simplify their model, they assume that the mug in question is rectangular and engaged in two-dimensional motion, i.e., motion perpendicular to the direction of the spring's action is absent. Because the coffee is initially at rest, the flow is always irrotational. "Our model considers sloshing in a tank suspended from a pivot that oscillates horizontally at a frequency close to the lowest sloshing frequency of the liquid in the tank," Ockendon said. "Together we have written several papers on classical sloshing over the last 40 years, but only recently were we stimulated by these observations to consider the pendulum effect."
The Ockendons focused on rectangular containers in and indicate that their mathematical study may be extended to include cylindrical cups in the future, but rest assured, the mathematical work won't stop there until cups of every possible geometry have been considered!
Still, while the maths that might lead to preventing sloshing and spilling may be terribly important for coffee drinkers, it's not the biggest math story of the year, so we much continue our search!
In the sport of basketball, the practical ability to skillfully place a round ball through an elevated circular ring with netting attached to it is one that can determine whether a player earns millions of dollars a season as a professional athlete or does not. Sometimes however, the limits of skilled players seem to stretch as they appear have an easier time in consistently shooting baskets than at other times, where they seem to have what's called a "hot hand" as they exceed their usual level of performance over an extended period of time during a game.
Scientists and statisticians have studied this apparent phenomenon over the years and have chalked it all up to randomness, where statistically speaking, it is something that periodically happens when a player's performance is much closer to the long end of the tails of a normal distribution describing their performance than it is to their mean performance, where the apparent "hot hand" is little more than a cognitive illusion as people who see it are really being fooled by randomness.
That consensus view was challenged in a paper by Joshua Miller and Adam Sanjurjo, who instead argue that earlier finding was based on a misreading of the math of probabilities.
Our surprising finding is that this appealing intuition is incorrect. For example, imagine flipping a coin 100 times and then collecting all the flips in which the preceding three flips are heads. While one would intuitively expect that the percentage of heads on these flips would be 50 percent, instead, it's less.
Here's why.
Suppose a researcher looks at the data from a sequence of 100 coin flips, collects all the flips for which the previous three flips are heads and inspects one of these flips. To visualize this, imagine the researcher taking these collected flips, putting them in a bucket and choosing one at random. The chance the chosen flip is a heads – equal to the percentage of heads in the bucket – we claim is less than 50 percent.
If flip 42 were heads, then flips 39, 40, 41 and 42 would be HHHH. This would mean that flip 43 would also follow three heads, and the researcher could have chosen flip 43 rather than flip 42 (but didn't). If flip 42 were tails, then flips 39 through 42 would be HHHT, and the researcher would be restricted from choosing flip 43 (or 44, or 45). This implies that in the world in which flip 42 is tails (HHHT) flip 42 is more likely to be chosen as there are (on average) fewer eligible flips in the sequence from which to choose than in the world in which flip 42 is heads (HHHH).
This reasoning holds for any flip the researcher might choose from the bucket (unless it happens to be the final flip of the sequence). The world HHHT, in which the researcher has fewer eligible flips besides the chosen flip, restricts his choice more than world HHHH, and makes him more likely to choose the flip that he chose. This makes world HHHT more likely, and consequentially makes tails more likely than heads on the chosen flip.
In other words, selecting which part of the data to analyze based on information regarding where streaks are located within the data, restricts your choice, and changes the odds.
Similar mathematical reasoning applies for the statistics behind the counterintuitive phenomenon described by the Monty Hall problem. It's a really cool insight, although one that we're afraid has limited potential for practical application, which is why we cannot call this the biggest math story of the year.
The field of mathematics is notorious for developing conjectures that defy proof for centuries. 2017 saw the delivery of a formal proof of the Kepler Conjecture, which identifies the maximum density by which spherical objects of equal size can be packed together within a given space, which was first proposed by Johannes Kepler in 1611. In the real world, the results can be seen anywhere spherically-shaped objects are packed together, such as oranges packed into a rectangular crate, which if optimally packed according to the Kepler Conjecture, will mean that a little over 74% of the available space will be filled by orange, while the rest of the space would be empty.
306 years later, a team of 19 researchers led by Thomas Hales appears to have finally cracked it and published a formal proof that can be confirmed by mathematician referees.
Or rather, by their computers, because Hales' team's proof is so sufficently complex that modern computing technology is the only way that humans have to verify the findings. In 2003, Hales anticipated that it would take 20-person years of labor for computers to verify every step of the proof in launching the project that finally delivered the proof 14 calendar years later.
Not every mathematical conjecture involving discrete geometry endures for centuries however. Some only last for decades, as was the case in Zilin Jiang's and Alexandr Polyanskii's proof of László Fejes Tóth’s zone conjecture, which says that if a unit sphere is completely covered by several zones, their combined width is at least equal to the irrational mathematical constant pi.
At first glance, these kinds of proofs may not seem to to have terribly practical applications, but effective solutions to discrete geometry problems like these do have real world impact.
Discrete geometry studies the combinatorial properties of points, lines, circles, polygons and other geometric objects. What is the largest number of equally sized balls that can fit around another ball of the same size? What is the densest way to pack equally sized circles in a plane, or balls in a containing space? These questions and others are addressed by discrete geometry.
Solutions to problems like these have practical applications. Thus, the dense packing problem has helped optimize coding and correct mistakes in data transmission. A further example is the four-color theorem, which says that four colors suffice to plot any map on a sphere so that no two adjacent regions have the same color. It has prompted mathematicians to introduce concepts important for graph theory, which is crucial for many of the recent developments in chemistry, biology and computer science, as well as logistics systems.
And also secure, garble-free, long distance (including interplanetary) communications, to name an up-and-coming application that would be an outcome for doing this kind of math!
Perhaps the biggest mathematical breakthrough honored in 2017 was the discovery by Maryanthe Malliaris and Saharon Shelah that two different variants of infinity, long thought to be different in nature, are actually equal in size.
In a breakthrough that disproves decades of conventional wisdom, two mathematicians have shown that two different variants of infinity are actually the same size. The advance touches on one of the most famous and intractable problems in mathematics: whether there exist infinities between the infinite size of the natural numbers and the larger infinite size of the real numbers.
The problem was first identified over a century ago. At the time, mathematicians knew that “the real numbers are bigger than the natural numbers, but not how much bigger. Is it the next biggest size, or is there a size in between?” said Maryanthe Malliaris of the University of Chicago, co-author of the new work along with Saharon Shelah of the Hebrew University of Jerusalem and Rutgers University.
In their new work, Malliaris and Shelah resolve a related 70-year-old question about whether one infinity (call it p) is smaller than another infinity (call it t). They proved the two are in fact equal, much to the surprise of mathematicians....
Most mathematicians had expected that p was less than t, and that a proof of that inequality would be impossible within the framework of set theory. Malliaris and Shelah proved that the two infinities are equal. Their work also revealed that the relationship between p and t has much more depth to it than mathematicians had realized.
Surprise is the right word, because Malliaris' and Shelah's result is very counterintuitional. And incredibly cool. But alas, not the biggest math story of 2017!
There is a class of mathematical problems named after Diophantus of Alexandria that are, unsurprisingly, known as Diophantine equations, whose components are made up of only sums, products, and powers in which all the constants are integers, and where the only solutions of interest are expressed as either integers or as rational numbers. If you think back to when you might have taken a class in algebra and recall those really wicked polynomial equations that you encountered or had to factor, that's the kind of problem that we're talking about.
Wicked being the operative word, because there's a really difficult Diaphantine equation that mathematicians have been working to solve for over four decades called the "cursed curve", where they've been seeking to prove that the equation only has a limited number of rational solutions. In November 2017, a team of mathematicians succeeded.
Last month a team of mathematicians — Jennifer Balakrishnan, Netan Dogra, J. Steffen Müller, Jan Tuitman and Jan Vonk — identified the rational solutions for a famously difficult Diophantine equation known as the “cursed curve.” The curve’s importance in mathematics stems from a question raised by the influential mathematician Jean-Pierre Serre in 1972. Mathematicians have made steady progress on Serre’s question over the last 40-plus years, but it involves an equation they just couldn’t handle — the cursed curve.
(To give you a sense of how complicated these Diophantine equations can get, it’s worth just stating the equation for the cursed curve: y4 + 5x4 − 6x2y2 + 6x3z + 26x2yz + 10xy2z − 10y3z − 32x2z2 − 40xyz2 + 24y2z2 + 32xz3 − 16yz3 = 0.)
In 2002 the mathematician Steven Galbraith identified seven rational solutions to the cursed curve, but a harder and more important task remained: to prove that those seven are the only ones (or to find the rest if there are in fact more).
The authors of the new work followed Kim’s general approach. They constructed a specific geometric object that intersects the graph of the cursed curve at exactly the points associated to rational solutions. “Minhyong does very foundational theoretical work in his papers. We’re translating the objects in Kim’s work into structures we can turn into computer code and explicitly calculate,” said Balakrishnan, a mathematician at Boston University. The process proved that those seven rational solutions are indeed the only ones.
"Kim's general approach" in this case refers to the work of the University of Oxford's Minhyong Kim, who has been working to apply concepts derived from the science of physics to the solution of difficult mathematical problems.
The proof for the seven solutions of the cursed curve is an exciting development for number theory, where the intersection of physics and mathematics brings us up to the biggest math story of the year.
We began this article with a discussion of the main difference between the standards of scientific proof and mathematical proof. Nowhere in 2017 is that difference more on display than in the biggest math story of the year, in which mathematicians have demonstrated that the famed Navier-Stokes equations that describe the flow of fluids in the real world, break down under "certain extreme conditions".
The Navier-Stokes equations capture in a few succinct terms one of the most ubiquitous features of the physical world: the flow of fluids. The equations, which date to the 1820s, are today used to model everything from ocean currents to turbulence in the wake of an airplane to the flow of blood in the heart.
While physicists consider the equations to be as reliable as a hammer, mathematicians eye them warily. To a mathematician, it means little that the equations appear to work. They want proof that the equations are unfailing: that no matter the fluid, and no matter how far into the future you forecast its flow, the mathematics of the equations will still hold. Such a guarantee has proved elusive. The first person (or team) to prove that the Navier-Stokes equations will always work — or to provide an example where they don’t — stands to win one of seven Millennium Prize Problems endowed by the Clay Mathematics Institute, along with the associated $1 million reward.
Mathematicians have developed many ways of trying to solve the problem. New work posted online in September raises serious questions about whether one of the main approaches pursued over the years will succeed. The paper, by Tristan Buckmaster and Vlad Vicol of Princeton University, is the first result to find that under certain assumptions, the Navier-Stokes equations provide inconsistent descriptions of the physical world.
By "inconsistent descriptions of the physical world", Buckmaster's and Vicol's work is pointing to the situation where, when given exactly the same fluid and starting conditions, instead of providing a single, unique solution for what the flow of fluids will be at a particular point of time in the future, the Navier-Stokes equations will instead provide two or more non-unique solutions, where they cannot accurately predict the future state of the resulting fluid flow.
That puts the physics associated with the Navier-Stokes equations into the situation where physicists and engineers must consider the limitations of where they can be shown to be valid in using them in their applications. Since Navier-Stokes is considered to be the "gold standard of the mathematical description of a fluid flow", that finding could potentially disrupt a whole lot of apple carts in multiple sciences and engineering disciplines whose applications might approach those limits.
That disruptive potential is why the story of the mathematical proof of the ability of the Navier-Stokes equations to describe unique solutions for all fluid flows under all conditions counts as being the biggest math story of 2017!
Previously on Political Calculations
The Biggest Math Story of the Year is how we've traditionally marked the end of our posting year since 2014. Here are links to our previous editions, along with our coverage of other math stories during 2017:
- The Biggest Math Story of the Year (2014)
- The Biggest Math Story of 2015
- The Biggest Math Story of 2016
- The Biggest Math Story of 2017
Have a Merry Christmas, and we'll see you again in the New Year!
Labels: math
Coming before a prolonged holiday week in the U.S., we suspect that this may be the least read of any post appearing on Political Calculations during 2017, but we'd like to knock it out before we go on our own year-end holiday, where we have just one more post after this one to present in 2017, in which we'll reveal the biggest math story of the year that was!
Until then however, let's check in with how our dividend futures-based forecasting model for the S&P 500 worked during the third full week of December 2017. The following chart shows where the actual trajectory of where the S&P 500 tracked against the background of our model's spaghetti-chart forecasts.
Week 3 of December 2017 is when the Tax Cuts and Jobs Act of 2017 officially became law, with President Trump signing the measure on Friday, 22 December 2017. Based on Federal Funds Rate futures, we believe that investors are currently mostly focusing on the first quarter in setting stock prices, where options speculators are betting that the Federal Reserve will act to boost short term interest rates in the U.S. again shortly before the end of that quarter.
We suspect that stock market investors are speculatively pricing in higher dividends in the future resulting from the tax cut, which have yet to materialize in the dividend futures themselves, where we are seeing the actual trajectory of the S&P 500 tracking along above the range we would expect if investors were closely focused on 2018-Q1 in setting stock prices based on the level of dividends that are currently projected for that future quarter.
That's not necessarily a bad speculation, where a number of U.S. firms have already announced that they will use the opportunity of the tax cut to increase the pay of their employees, whether through bigger paychecks or through bonuses.
We'll find out, most likely in 2018 after the boards of directors of S&P 500 companies have had the chance to meet and make decisions on how they might adapt their compensation and dividend payout policies to respond to the tax cut, how smart that speculation may be.
Until then, for our last post looking at the S&P 500 of 2017, we'll close by wrapping up the week's market moving headlines in the following package....
- Monday, 18 December 2017
- Tuesday, 19 December 2017
- Wednesday, 20 December 2017
- Thursday, 21 December 2017
- Friday, 22 December 2017
Elsewhere, Barry Ritholtz succinctly summarized the positives and negatives for the U.S. economy and markets for Week 3 of December 2017.
That's it for now - we'll be back sometime tomorrow with our special last post of 2017!
The city of Philadelphia's controversial soda tax is providing a lot of material for serious scientists to evaluate the effects of arbitrarily imposing a tax on the distribution of a range of naturally and artificially-sweetened beverages. Since we're near the end of the tax's first year of being in effect, we thought we'd focus upon one of the more interesting findings to date.
Consumers are primarily the ones paying the tax
Thanks to the quirks of geography and development, some parts of the terminals at Philadephia's international airport fall within Philadelphia's city limits while other parts do not, which means that Philadelphia's Beverage Tax is imposed in some parts of the airport while not in others. Cornell University's John Cawley recognized that situation would make for a natural experiment for assessing some of the impact of the tax, where they collected data for soda sales at the airport in the period of December 2016 through February 2017, which provides a window into how both prices and sales changed as the tax went into effect on 1 Janaury 2017. Here's a summary of the research's findings:
The research, co-written with Barton Willage, a doctoral candidate in economics, and David Frisvold of the University of Iowa, appeared Oct. 25 in JAMA: The Journal of the American Medical Association.
Philadelphia’s tax of 1.5 cents per ounce on sugar-sweetened beverages is one of several passed by cities throughout the United States. The goal is to increase prices and dissuade people from drinking soda to benefit their health. These taxes have been controversial; Cook County, Illinois, recently repealed its tax, which had only been in place a few months.
The Philadelphia tax (and one in Berkeley, California) are levied not on consumers but on distributors. That’s because lawmakers are trying to change consumers’ behavior but want, for political reasons, to avoid taxing consumers directly. So they levy the tax farther up the supply chain, said Cawley, who is co-director of Cornell’s Institute on Health Economics, Health Behaviors and Disparities.
Until now, it has been unclear just how much of Philadelphia’s tax on distributors would be passed on to consumers in the form of higher retail prices. Distributors could just pay it themselves to avoid a decrease in sales, Cawley said. “Or producers like Coke and Pepsi could say, ‘We’re not going to let cities use this tax to decrease our sales; we’re going to bear the brunt of it. We’ll just sell our soda cheaper to distributors, and that’s how we’ll keep retail prices the same,’” he said.
But in Philadelphia, just 36 days after the tax went into effect, stores raised their retail soda prices by a whopping 93 percent of the tax. “I was surprised by how much of the Philadelphia tax was passed on to consumers in such a short period time,” said Cawley.
And some untaxed airport stores, technically located in Tinicum, Pennsylvania, also raised their prices by exactly the amount of the tax after the taxed stores did, the study found. “It was impossible to predict in advance whether the untaxed side of the airport would limit the pass-through of the tax on the Philadelphia side, or whether the untaxed side would take advantage of Philadelphia’s tax to raise prices themselves,” says Cawley.
The 93 percent “pass-through” to Philadelphia consumers was significantly higher than occurred in Berkeley, California; previous research (including some by Cawley and Frisvold) showed that only 43 to 69 percent of the Berkeley tax was passed on to soda drinkers there.
This finding is highly significant because although Philadelphia directly imposes the tax on beverage distributors in the city (the de jure incidence of the tax), in reality, the tax is predominantly falling upon consumers, who are the ones who are primarily paying the tax (this is the de facto incidence of the tax).
The true incidence of the tax matters because it potentially affects the legality of the tax and how it is imposed. The imposition of a similar soda tax in Chicago was largely derailed because courts in that state recognized the de facto nature of the tax, while courts in Pennsylvania have so far dismissed the real world incidence of the tax in upholding Philadelphia's soda tax. Pennsylvania's state supreme court has not yet announced whether it will hear an appeal of the case.
Meanwhile, the pass-through of 93% of Philadelphia's soda tax to consumers at Philadelphia's International Airport falls on the high side of our own observations throughout 2017, where overall, we've found that two-thirds of Philadelphia's soda tax is being passed through to consumers.
Confounding factors for soda prices on the Tinicum-side of the airport
We should however recognize that the market represented by Philadelphia's International Airport is not generally representative of the market for beverages in the city, where the airport cannot be considered to provide a genuinely free market for competition. For example, the city of Philadelphia, which manages the airport, is able to severely restrict the number of vendors that may do business at the airport.
Restricting the ability of outside vendors to freely enter into the market represented by Philadelphia's international airport allows the approved vendors who sell soft drinks outside of Philadelphia's city limits at the airport to hike the prices of the sweetened beverages they sell without the potential penalty of losing business to competitors charging lower prices, with the vendors and their employees pocketing the difference thanks to their city-granted, monopoly-like business privilege.
On average, in December 2016 before the tax was implemented, the mean price per ounce of cola was 12.37 cents on the untaxed side and 12.53 cents per ounce in the taxed side. By February 2017, that price had increased to 12.93 on the untaxed side and 13.92 on the taxed side. Thus, the price had risen significantly more on the taxed side.
The investigators calculated that overall, 55.3 percent of the tax was passed along to consumers. In the taxed stores, however, 93 percent of the tax was passed to consumers by February.
One might query why the stores in the untaxed part of the airport also raised prices? Probably because they could, and it would simply add to their profits.
That would make logical sense, but there's more to the story, where the common conflating factor of the intervention of Philadelphia's city government is also at work. Here, the role of the city in jacking up prices for consumers at parts of the airport outside of the city's limits was confirmed by the mayor's office.
Mike Dunn, a spokesman for Mayor Kenney, said Friday that vendors on the Tinicum side who have raised their prices since Jan. 1 did so for a different reason. Three out of the 37 vendors in Tinicum received permission to change prices this year, Dunn said, and all did so as part of a voluntary program that allowed them to raise all prices by 10 percent in exchange for paying their employees more.
All airport merchants will be required to pay a minimum hourly wage of $12.10 when they enter new concession contracts, Dunn said, but three vendors on the Tinicum side elected to begin early.
That dynamic adds an interesting wrinkle to Cawley's initial research findings, one where he should already have the detailed data indicating the amount of prices changes of soda at all airport locations to be able to resolve, where it should be easy to identify the vendors that increased their soda prices by the 10% that was blessed by the mayor's office. How soda prices changed at the remaining vendors will then give us an ideal of the extent to which those other vendors took advantage of the opportunity to gouge their customers within the closed market of the Philadelphia International Airport during the first two months of the tax going into effect.
It's a question to which we don't yet know the answer that will be exciting to find out, hopefully in 2018!
Labels: economics, food, taxes
The data for December 2017 is preliminary, but since we're coming up on the end of the year, we couldn't resist updating one of our favorite charts showing the periods of relative order and chaos in the S&P 500 since December 1991!
If you would like to access the data for any of the months for which we've have finalized data in the above chart, or for that matter, for any month since January 1871, we make it available through our S&P 500 At Your Fingertips tool, which will also indicate the rates of return, both with and without the effects of inflation and dividend reinvestment, between any two calendar months within our dataset.
Labels: chaos, data visualization, SP 500
Are you ready to peer into the future for the S&P 500's quarterly dividends per share in 2018?
If so, you've come to the right place! The following chart shows the snapshot we took of the CME Group's S&P 500 Quarterly Index Dividend Futures Quotes for each quarter in 2018 on 18 December 2017, and for good measure, compares it to a snapshot we took of similar dividend futures presented by the Chicago Board of Exchange a year earlier showing what the future for 2017 was expected to be at the same relative point of time in that year. (The CBOE retired their implied forward dividend futures on 1 May 2017).
2017 was the best year for dividends on record for the S&P 500. 2018 looks to be stronger, but then, that's a primary reason why stock prices have generally grown so strongly throughout the year.
One thing to note is that these are dividend futures, which do not match the quarterly dividends reported by Standard and Poor after the end of each calendar quarter. That is because of what we describe as the term mismatch between the two, where the indicated dividends shown in the chart above are tied to futures contracts that run from the end of the third Friday of the month in the preceding quarter through the third Friday of the month ending the indicated quarter, while the values reported by S&P occur solely within each calendar quarter.
The difference between the two are most evident in the data for Q4 and Q1, where the dividend futures for Q4 tend be understated and the values for Q1 tend be overstated when compared with the values reported by S&P, which is due to larger dividend payments that are paid out to shareholders in the final weeks of each year. To give you an idea of how much that adjustment can be, we anticipate that the S&P 500's quarterly dividends in 2017-Q4 will come in around $12.70 per share when S&P reports them in the new year.
Labels: dividends, forecasting, SP 500
Even though the Federal Reserve's Federal Open Market Committee voted to hike short term interest rates in the U.S. by a quarter percent on Wednesday, 13 December 2017, the biggest news of the week, as far as the U.S. stock market was concerned, came on Friday as the congressional majority Republicans announced they had reached a compromise between the House and Senate versions of the corporate income tax cut bill, where a vote would be scheduled during the next week.
Combined with the news that Senate Republicans who had been holding out support for the bill, which will also reduce personal income taxes for a majority of working Americans, were going to support the compromise, investors provided the S&P 500 with what we would describe as a noisy speculative boost on Friday, 15 December 2017.
Overall, although our chart shows stock prices seeming to follow along the alternative trajectory associated with investors being focused on 2018-Q2, we think that they are really focused on 2018-Q1, which would coincide with the most likely timing of the Fed's next expected rate hike, where the positive speculative noise from the tax cut deal is boosting the S&P 500 to the top end of the range that we would expect if they were primarily focused on that future quarter.
Meanwhile, we weren't kidding when we said that there wasn't much other news of note that could drive the market in the second full week of December 2017. Here are the headlines that we felt qualified as noteworthy during the week that was.
- Monday, 11 December 2017
- Tuesday, 12 December 2017
- Wednesday, 13 December 2017
- Thursday, 14 December 2017
- Oil prices up on pipeline outage support
- QE Lives!: U.S. Fed buys $4.4 billion of mortgage bonds, sells none
- Believe it when you see it from the gang that can't shoot straight: Republicans forge tax deal, final votes seen next week
- Wall Street falls as investors fret about tax bill passage
- Friday, 15 December 2017
- Oil hovers below two-year highs with focus on U.S. output
- Fed's Evans says voted against rate hike over inflation concerns
- Republicans have finalized compromise U.S. tax bill -chief House tax writer
- Last minute holdout ends: Republican Senator Rubio will back tax bill: CNBC, citing sources
- Last holdout ends: Republican Senator Corker says he will support tax bill
- Wall Street closes at records with tax overhaul in sight
Finally, Barry Ritholtz lists the positives and negatives for the U.S. economy and markets in a succinct summary of the markets and economy news for Week 2 of December 2017.
President Donald Trump drinks a lot of Diet Coke, where according to the New York Times, his daily consumption consists of as many as twelve 12-ounce cans of the artificially-sweetened, zero-calorie carbonated beverage.
That report has sent CNN into a frenzy, where the cable news channel prioritized that story over the story of the attempted terrorist pipe bomb attack in New York City's subway in its televised broadcasts on the same day.
But since that story raised questions about President Trump's health, where the effects of that apparently high level of Diet Coke consumption were called into question. The Washington Post was sucked into the story, providing a general overview of what the medical profession knows about the potential health-related risks that might arise from drinking that many cans of diet soda a day, and came away with not much insight.
It's a lot of soda to consume in one day, and — were it regular soda — most research suggests the potential consequences would be alarming. A 12-ounce can of regular Coke has 140 calories and 39 grams of sugar. By instead drinking Diet Coke, which has no calories or sugar, Trump has avoided consuming 1,680 calories and 468 grams of sugar daily.
But the effects of drinking diet soda have been long debated by experts, with some studies raising concerns about long-term health consequences. Experimental research on artificial sweeteners, like the ones found in diet soda, is inconclusive. The Canadian Medical Association Journal found in July that there are very few randomly controlled studies on artificial sweeteners — just seven trials involving only about 1,000 people — that looked at what happened when people consumed artificial sweeteners for more than six months.
Overall, most medical risks associated with high levels of diet soda consumption would appear to be very low, with the potential exception of two of its ingredients, caffeine and aspartame, where the Food and Drug Administration (FDA) and the European Food Safety Authority (EFSA) have set levels for Acceptable Daily Intake (ADI), which "is defined as the maximum amount of a chemical that can be ingested daily over a lifetime with no appreciable health risk, and is based on the highest intake that does not give rise to observable adverse effects".
We did some digging and found that the FDA sets the ADI for caffeine* at 6 milligrams per kilogram of body weight per day (the EFSA sets the limit for children at half that level). Meanwhile, the FDA sets the ADI limit for aspartame, which is branded as "NutraSweet", at 50 milligrams per kilogram of body weight per day, where the EFSA sets it at 40 mg/kg/day.
That gives us enough information to be able to estimate how many cans of Diet Coke that President Trump, or for that matter, anybody, can safely drink per day to keep a low risk of adverse health effects.
So we have! In the following tool, we've used Diet Coke specific data to estimate the number of 12-ounce cans of that beverage that you might get away with drinking each day, but you are welcome to change the data to consider whatever beverage containing caffeine or aspartame you might consider drinking to work out how many units per day that you can consume within the FDA's acceptable daily intake levels. If you're accessing this article on a site that republishes our RSS news feed, please click here to access a working version of the tool on our site.
Using the tool, with the default data body weight set to be equal to what President Trump was reported to weigh at this writing in December 2017, we find that while President Trump could drink nearly 30 cans of Diet Coke and stay under the FDA's ADI guidelines for aspartame, his real daily limit is to drink the equivalent of no more than 13.8 12-ounce cans of Diet Coke per day, which would keep him within the FDA's ADI limits for "safe" caffeine consumption. At the reported dozen cans of diet soda drunk per day, President Trump is falling within those limits for his body weight.
Playing with the tool, we find that if President Trump were to lose more than 31 pounds, he would need to reduce his daily diet soda consumption to stay within the FDA's safe limits for daily caffeine intake.
As they say, it is the dose that makes the poison for any ingestible substance. Things like the concentration of ingredients within the substance being consumed and the size of the person doing the ingesting are just two of the factors that can affect the determination of what is an okay amount of consumption of any substance for an individual.
Speaking of which, the biggest factor that we haven't considered with this tool is whether diet soda is your only source for your daily caffeine and aspartame intake. The extent to which you may be ingesting additional caffeine or aspartame through other foods, beverages, medicines, etc. would reduce the amount that you would need to consume in the form of diet soda to stay within the FDA's or EFSA's guidelines.
If you don't know that extent, we would argue that it would be prudent to significantly dial back on your diet soda consumption to ensure that you don't accidentally run into the situation where you experience any of the adverse health effects that are the reason for why the ADI guidelines exist in the first place.
* Update 18 December 2017: We did some additional digging and found that the FDA doesn't actually set an Acceptable Daily Intake level for caffeine and instead simply considers it to be "generally recognized as safe". The 6.0 mg/kg/day figure appears to come from a 2003 study, which identifies a 400 mg/day "safe" intake limit for a healthy individual who weighs 65 kg (143 lb), which is fully consistent with the 6.0 mg/kg/day intake level. This study is very likely the source of the FDA's subsequent identification of 400 mg of caffeine per day as the "safe" daily intake level for adults, where the FDA may very well have lost track of how and for what weight individual that latter figure was determined in the years since 2003.
References
Nawrot, P., Jordan, S., Eastwood, J., Rotstein, J., Hugenholtz, A., Feeley, M. Effects of caffeine on human health. Food Addit Contam. 2003 Jan; 20(1):1-30. DOI: 10.1080/0265203021000007840.
Labels: food, health, risk, tool
The Federal Reserve did the completely expected yesterday and announced that it would increase the Federal Funds Rate, the interest rate that U.S. banks charge when loaning money to other banks overnight, by a quarter percent, raising its target range for the Federal Funds Rate to now be between 1.25% to 1.50%.
Using the FOMC's announcement to take a snapshot in time of the probability of recession in the United States, we find that through 13 December 2017, it has ticked slightly up from our last report to 0.40%.
With the Federal Funds Rate still effectively set at 1.16% (the midpoint of the FOMC's previous target range between 1.00% and 1.25%) and the slightly declining spread in the yields between the 10-year and 3-month constant maturity U.S. Treasuries, the probability of a recession occurring within the next 12 months dropped just a fraction of a percentage point to 0.40% from the 0.37% where we last estimated it.
As such, there is currently very little chance that the National Bureau of Economic Research will someday declare that a national recession began in the U.S. between now and 13 December 2018 according to Jonathan Wright's recession forecasting methods.
That doesn't mean however that all parts of the U.S. will be recession free. As we've seen in recent years, parts of the U.S. may indeed experience what we've described as a microrecession, where some degree of economic contraction has occurred, but which lacks the combination of scale, scope and duration needed for the NBER to recognize a recession at the national level.
Previously on Political Calculations
Labels: recession forecast
When it comes to the health of his state's economy, California Governor Jerry Brown has been walking on eggshells this year.
Twice each year, once in January and again in May, Gov. Jerry Brown warns Californians that the economic prosperity their state has enjoyed in recent years won't last forever.
Brown attaches his admonishments to the budgets he proposes to the Legislature – the initial one in January and a revised version four months later.
Brown's latest, issued last May, cited uncertainty about turmoil in the national government, urged legislators to "plan for and save for tougher budget times ahead," and added:
"By the time the budget is enacted in June, the economy will have finished its eighth year of expansion – only two years shorter than the longest recovery since World War II. A recession at some point is inevitable."
It's certain that Brown will renew his warning next month. Implicitly, he may hope that the inevitable recession he envisions will occur once his final term as governor ends in January, 2019, because it would, his own financial advisers believe, have a devastating effect on the state budget.
Unfortunately for Governor Brown, the recession he fears may already have arrived in California.
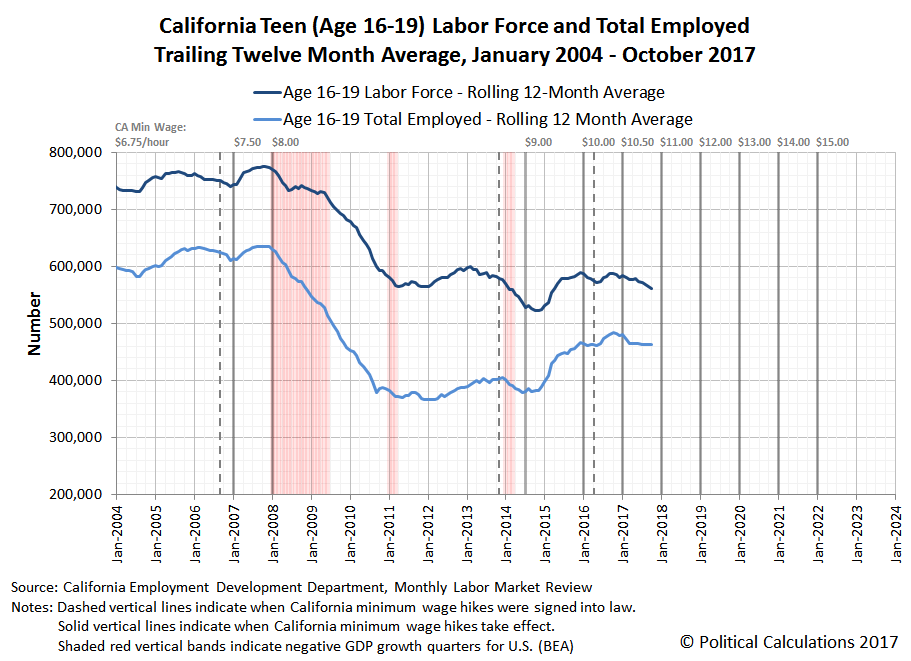
The following chart showing the trailing twelve month averages of California's civilian labor force and number of employed is one that we've adapted from a different project to show that data in the context of the state's higher-than-federal minimum wage increases and periods of negative GDP growth for the national economy. It shows that in 2017, the size of the state's labor force has peaked and begun to decline in 2017, while the number of employed shows very slow to stagnant growth during the year.
The data for this chart is taken from the summary tables for the state's monthly reports on the California Demographic Labor Force, which are produced by California's Employment Development Department. These are therefore the same numbers that Governor Brown sees, and they have been signaling throughout 2017 that the state's economy is going through a period of stagnation after having generally grown since bottoming in mid-2011 following the Great Recession.
The labor force and employment numbers aren't telling the full story however, which becomes evident when we factor in the state's growing population. The following chart shows the labor force and employment to population ratios for the state's civilian work force.
In this chart, we find that California's employment to population ratio peaked at 59.2% in December 2016, having slowly declined to 59.0% through October 2017. Meanwhile, California's labor force to population ratio last peaked at 62.6% in October 2016, which has since dropped to 62.1% a year later.
Going by these measures, it would appear that recessionary conditions have arrived in California, which is partially borne out by state level GDP data from the U.S. Bureau of Economic Analysis:
Last year was a very good one for the state’s economy. The 3.3 percent gain in economic output in 2016 was more than double that of the nation as a whole and one of the highest of any state.
However, California stumbled during the first half of 2017. California’s increase was an anemic six tenths of one percent in the first quarter compared to the same period of 2016, and 2.1 percent in the second quarter, well below the national rate and ranking 35th in the nation.
The report revealed that almost every one of California’s major sectors fell behind national trends in the second quarter, with the most conspicuous laggard being manufacturing.
On a final note, the charts we've featured above were adapted from our project tracking the impact of California's minimum wage hikes on its teen labor force, where we've been following that labor force and employment data since July 2003 (which hopefully helps explain why the trailing 12 month labor force and employment to population ratio chart starts showing data beginning in June 2004). As bad as the charts above are for California's labor force, the employment situation for California's teens is much worse, having itself peaked in October 2016.
California's teens are best thought of as being the proverbial canaries in the coal mine.
Update 26 December 2017 11:41 AM PST: Changed "recession has" to "recessionary conditions have" above (about six paragraphs up), which better describes how we're considering the data that we've seen to date. Also, if you came to this article by way of ZeroHedge, which has rather completely surprised us in recent weeks by picking up and republishing a number of our recent posts (including two on the topic of Philadelphia's soda tax), our outlook for the state of the economy is not anywhere near as gloomy, doomy or as conspiratorial as the worldview that we associate with a lot of ZH's content.
That said, even though the republished articles have come without any coordination or even notice, we appreciate the Tyler Durdens making some of our content available to their estimated 4 million unique readers each month. And though they might have the most dismal outlooks of all, at least they're not some strange breed of creepy cyber-stalkers!
Labels: recession
How well are typical American households faring through the third quarter of 2017?
To answer that question, we're going to turn to a unique measure of the well-being of a nation's people called the national dividend. The national dividend is an alternative way to measure of the economic well being of a nation's people that is primarily based upon the value of the things that they choose to consume in their households, which makes it very different and by some accounts, a more effective measure than the more common measures that focus upon income or expenditures throughout the entire economy, like GDP, which have proven to not be well suited for the task of assessing the economic welfare of the people themselves.
To get around that problem, we've developed the national dividend concept that was originally conceived by Irving Fisher back in 1906, but which fell by the wayside in the years that followed because the government proved to not be capable of collecting the kind of consumption data needed to make it a reality for decades. And then, it wasn't until we got involved in 2015 that anybody thought to try it, where we've been able to make the national dividend measure of economic well-being into a reality.
With that introduction now out of the way, let's update the U.S.' national dividend through the end of September 2017 following our previous snapshot which was taken for data available through April 2017.
We find that the third quarter of 2017 has seen some of the most robust increases in the national dividend in 2017, which itself has been an improvement over what happened to it in 2016, where the national dividend actually declined in the latter half of that year.
Notes
This is the first update that we've had since June 2017, which is a direct consequence of Sentier Research's termination of its monthly household income estimates data series after May 2017. We had suspended our presentation of our national dividend estimates until we developed a viable substitute for this original data source, which we've been test driving for this application behind the scenes.
What we've found so far is that our estimates for the national dividend are conservative in the period from 2015 onward, in that we believe that they are understating the amount of consumption by U.S. households, which we believe is a consequence of a change in methodology by the U.S. Census Bureau for how it collects the source data we use in our calculations. We do not as yet have enough data to establish the extent to which our estimates of national income may be understated, which we're continuing to collect and review behind the scenes. We do believe however that our measure is capturing the overall picture for the direction of the national dividend, which perhaps is a more useful indication of the relative well-being of typical American households that can be determined by this kind of analysis.
Previously on Political Calculations
The following posts will take you through our work in developing Irving Fisher's national dividend concept into an alternative method for assessing the relative economic well being of American households.
- Calculating the National Dividend - we revive Irving Fisher's concept for calculating a "national dividend".
- The National Dividend vs GDP - perhaps the best way to think of the national dividend is that it is the part of GDP that filters through to regular American households. As such, it's the part of GDP that matters.
- An Almost Perfect Correlation - we discover a unique relationship that enables our subsequent work to make the national dividend into a near-real time measure of the economic well-being of American households.
- Developing the National Dividend Into a Monthly Economic Indicator - just that!
- The National Dividend in 2015-Q2
- Replacing GDP with the National Dividend - our anniversary post from 2015!
- Calculating the U.S. National Dividend through April 2016
- Update: The National Dividend Through December 2016
- The U.S. National Dividend Through April 2017
References
Chand, Smriti. National Income: Definition, Concepts and Methods of Measuring National Income. [Online Article]. Accessed 14 March 2015.
Kennedy, M. Maria John. Macroeconomic Theory. [Online Text]. 2011. Accessed 15 March 2015.
Political Calculations. Modeling U.S. Households Since 1900. 8 February 2013.
U.S. Bureau of Labor Statistics. Consumer Expenditure Survey. Total Average Annual Expenditures. 1984-2015. [Online Database]. Accessed 7 February 2017.
U.S. Bureau of Labor Statistics. Consumer Price Index - All Urban Consumers (CPI-U), All Items, All Cities, Non-Seasonally Adjusted. CPI Detailed Report Tables. Table 24. [Online Database]. Accessed 15 November 2017.
Labels: data visualization, economics
Welcome to the blogosphere's toolchest! Here, unlike other blogs dedicated to analyzing current events, we create easy-to-use, simple tools to do the math related to them so you can get in on the action too! If you would like to learn more about these tools, or if you would like to contribute ideas to develop for this blog, please e-mail us at:
ironman at politicalcalculations
Thanks in advance!
Closing values for previous trading day.
This site is primarily powered by:
CSS Validation
RSS Site Feed
JavaScript
The tools on this site are built using JavaScript. If you would like to learn more, one of the best free resources on the web is available at W3Schools.com.