We've come to the end of 2022, making it time to take stock of the biggest math stories of the year that was!
In choosing these stories, we've emphasized math stories involving practical applications in selecting the contenders for the Biggest Math Story of 2022, which we'll present at the end of this year's edition. But before we get started, let's take a minute to do something mathematical that has no direct practical application but which is surprisingly satisfying by watching the following video visualizing the first million integers and coloring them by their prime factors.
There is a practical application in John Williamson's integer mapping exercise, which is the UMAP data visualization tool used to make this short video. UMAP is the acronym for Uniform Manifold Approximation and Projection, which can be applied to large datasets to help make better sense of the information within them in the growing field of visual analytics.
This introduction is already working on several different levels. Intentionally. Most obviously, it's the beginning of the longest article we write each year. It's also provided the opportunity to introduce a practical application that came about from maths that were originally developed as little more than intellectual curiosities. Maths that weren't very practical until the applications they enabled made them essential. The Biggest Math Story of 2022 involves what we'll describe in this introduction as the ultimate application arising from what some describe as most unlikely math.
We'll get there soon enough. Because the Biggest Math Story of 2022 serves as our final article of the year, we've written it to be read and revisited as you might like throughout the holidays. You can take your time to explore the stories and follow the links to go deeper into the various topics. Or you can just blow past all the sections and go straight to the Biggest Math Story of 2022 so you have something extra smart to talk about at holiday parties. Let's get to it....
Artificial Intelligence Discovers Faster Math
Picking up from where we left off with the biggest math story of 2021, artificial intelligence continued to make inroads in powering mathematical discoveries, even as the technology made bigger headlines during the year in other fields, including in art and writing.
Perhaps the most notable accomplishment after last year's major achievements by the DeepMind team was the discovery of a faster, more efficient method for multiplying matrices. And they did it by making a game out of doing the math:
The DeepMind team approached the problem by turning tensor decomposition into a single-player game. They started with a deep learning algorithm descended from AlphaGo — another DeepMind AI that in 2016 learned to play the board game Go well enough to beat the top human players.
Using that base, they developed a new agent called AlphaTensor to play their matrix multiplication game. The DeepMind team summarized their approach in the paper announcing their accomplishment:
Here we report a deep reinforcement learning approach based on AlphaZero for discovering efficient and provably correct algorithms for the multiplication of arbitrary matrices. Our agent, AlphaTensor, is trained to play a single-player game where the objective is finding tensor decompositions within a finite factor space. AlphaTensor discovered algorithms that outperform the state-of-the-art complexity for many matrix sizes. Particularly relevant is the case of 4 × 4 matrices in a finite field, where AlphaTensor’s algorithm improves on Strassen’s two-level algorithm for the first time, to our knowledge, since its discovery 50 years ago.
That has the makings of being a big deal, but as the researchers acknowledge, their accomplishment is limited in its utility:
Researchers also emphasized that immediate applications of the record-breaking 4-by-4 algorithm would be limited: Not only is it valid only in modulo 2 arithmetic, but in real life there are important considerations besides speed.
Here's a basic introduction to modular arithmetic, where Modulo 2 arithmetic is the type that deals exclusively with zeroes and ones. Although not mentioned in this story, important considerations other than speed in doing calculations include things like precision and accuracy.
Meanwhile, if you're wondering about the illustration for this section, we generated it using Stable Diffusion's 2.1 Demo, using the prompt "artificial intelligence finds a faster way to multiply matrices". If you think about it, it's an AI telling us what another AI looks like!...
Finding the Limits of Math That Can Be Done
The limitations of the AI-developed matrix multiplication algorithm point toward another of the big challenges mathematicians took on in 2022. Specifically, the challenges associated with determining when calculations can be done with confidence they'll deliver good results and identifying the limits where they stop working well.
The biggest math story in this category involves a new proof that also relied upon advanced computing techniques to find out when and under what conditions Euler's equations describing fluid mechanics might "blow up".
In this case, "blowing up" means the math breaks down and starts providing results that are violently unstable. That's similar to the situation where you have a simple fraction with zero in the denominator, the result for which is undefined when you attempt to perform the implied division operation. But as you're about to see, that's not the only challenge associated with the proof that's been advanced:
In a preprint posted online last month, a pair of mathematicians has shown that a particular version of the Euler equations does indeed sometimes fail. The proof marks a major breakthrough — and while it doesn’t completely solve the problem for the more general version of the equations, it offers hope that such a solution is finally within reach. “It’s an amazing result,” said Tristan Buckmaster, a mathematician at the University of Maryland who was not involved in the work. “There are no results of its kind in the literature.”
There’s just one catch.
The 177-page proof — the result of a decade-long research program — makes significant use of computers. This arguably makes it difficult for other mathematicians to verify it. (In fact, they are still in the process of doing so, though many experts believe the new work will turn out to be correct.) It also forces them to reckon with philosophical questions about what a “proof” is, and what it will mean if the only viable way to solve such important questions going forward is with the help of computers.
You know you're on the bleeding edge of progress in maths when new questions like these are being raised!
Should the new proof hold, it marks a major development toward determining if the more general Navier-Stokes fluid dynamics equation could be similarly vulnerable to blowing up as well. The challenge of answering that question is the subject of one of the Clay Mathematics Institute's Millennium Prize Problems, where the mathematicians who definitively determine if there are or if their are not any conditions that could cause the equation to blow up will win a $1 million prize. There's been a lot of mathematicians nibbling around the edges for resolving that question, but with no results confirmed as yet.
Approximate and Exact Solutions
When we write up the biggest math story of the year, we're really seeking out the biggest math story that offers real practical application. During the year, we featured a story with that headline about such an application that involved finding a simple and relatively accurate approximation to math that might otherwise require more significant computing resources to obtain results.
Here, several chemists realized that the calculus integral developed by epidemiologial pioneers W. O. Kermack and A. G. McKendrick to describe how a contagious disease might propagate through a population was identical to the math used to describe the progress of an autocatalytic reaction in chemistry. That integral has no direct solution, but it happened to be math for which they developed an approximate algebraic formulation to solve problems involving autocatalytic reactions that they realized could be applied to quickly solve the Kermack-McKendrick integral with a small margin of error.
One of the authors described how they found the connection:
Dr. Baird presented the model in May at the Southeastern Theoretical Chemistry Association meeting in Atlanta.
"The World Health Organization could program our equation into a hand-held computer," Dr. Baird says. "Our formula is able to predict the time required for the number of infected individuals to achieve its maximum. In the chemical analog, this is known as the induction time."
The formula is capable of predicting the number of hospitalizations, death rates, community exposure rates and related variables. It also calculates the populations of susceptible, infectious and recovered individuals, and predicts a clean separation between the period of onset of the disease and the period of subsidence....
"The rate of infection initially accelerates until it reaches a point where the infection rate is balanced by the recovery rate of infected individuals, at which point the number of infected people peaks and then starts to decay," he says.
That mechanism reminded him of the mechanism that governs an autocatalytic reaction.
"I subsequently learned that the mathematical description of the spread of infectious diseases was first described by Kermack and McKendrick," Dr. Baird says.
"When I read their paper, I realized that their mechanism was exactly the same as that of an autocatalytic reaction, where a catalyst molecule combines with a reactant molecule to produce two catalyst molecules," he says. "The rate of production of catalyst molecules accelerates until it is balanced by the rate of decay of the catalyst to form the product."
This story is also about the tradeoff between accepting small errors in return for obtaining reasonably accurate results with speed. But what if you could develop a formula that provided an exact solution?
That scenario is playing out at the University of Bristol, where the math needed to realistically modeling the process of diffusion has been developed by Toby Kay, an engineering mathematics PhD student, and Dr. Luca Giuggioli, who has been working on the math of diffusion for some time.
A groundbreaking mathematical equation that could transform medical procedures, natural gas extraction, and plastic packaging production in the future has been discovered.
The new equation, developed by scientists at the University of Bristol, indicates that diffusive movement through permeable material can be modeled exactly for the very first time. It comes a century after world-leading physicists Albert Einstein and Marian von Smoluchowski derived the first diffusion equation, and marks important progress in representing motion for a wide range of entities from microscopic particles and natural organisms to man-made devices.
Until now, scientists looking at particle motion through porous materials, such as biological tissues, polymers, various rocks and sponges have had to rely on approximations or incomplete perspectives.
The findings, published today in the journal Physical Review Research, provide a novel technique that presents exciting opportunities in a diverse range of settings including health, energy, and the food industry.
Here's a sampling of where the new diffusion math described in their paper might be applied in its next steps:
Further research is needed to apply this mathematical tool to experimental applications, which could improve products and services. For example, being able to model accurately the diffusion of water molecules through biological tissue will advance the interpretation of diffusion-weighted MRI (Magnetic Resonance Imaging) readings. It could also offer more accurate representation of air spreading through food packaging materials, helping to determine shelf life and contamination risk. In addition, quantifying the behavior of foraging animals interacting with macroscopic barriers, such as fences and roads, could provide better predictions on the consequence of climate change for conservation purposes.
That's a lot of exciting potential, but doesn't qualify as the Biggest Math Story of 2022. For that, you'll need to read on....
Persistence and Dedication
In assembling the Biggest Math Story of the year, we often discover themes or trends that make the year stand out from others. In 2018, it was the role of amateurs in advancing mathematical knowledge. In 2019, social media proved to be an enabling factor in many of the year's bigger math stories. 2020 was completely defined by the failure of the world's premier epidemiological models to forecast the coronavirus pandemic. And we've already mentioned 2021 as the year artificial intelligence contributed to significant mathematical discoveries.
We think the underlying theme for 2022 is persistence and dedication. Like 2018, amateurs made some very practical advances, including high school students like Glenn Bruda, who identified an improved method for integrating complex equations and Daniel Larsen, who developed a proof for a theorem about the distribution of Carmichael numbers, also known as "pseudoprime" numbers, which parallels work being done by well established mathematicians to crack number theory's "twin prime" conjecture. When you dig into these stories, these achievements are the result of these amateur mathematicians' unusual persistence and dedication.
But it's not just amateurs. We found the story of how mathematicians Eric Larson and Isabel Vogt solved a several hundred year-old conjecture about algebraic curves to be unusually charming. Here's an excerpt from Quanta Magazine's Jordana Cepelwicz' story on their discovery:
... in a proof posted online earlier this year, two young mathematicians at Brown University, Eric Larson and Isabel Vogt, have finally dealt the problem its final blow, solving it completely and systematically. The paper marks the culmination of nearly a decade of work, during which they gradually chipped away at the question, solved important related problems about what curves look like and how they behave — and also got married.
“It’s really a remarkable story,” said Sam Payne, a mathematician at the University of Texas, Austin, “for [people] that young and that early in their mathematical development to latch on to such a deep, hard problem, and then to be so persistent.”
The best part of the story is its revelation that Larson and Vogt keep chalkboards in their home so they can work on problems. If you know anything about mathematicians and their love of chalk, you appreciate their dedication!
Then again, they are professional mathematicians! Pure mathematics, as done by professional mathematicians, often doesn't directly connect to practical applications. But when it does, the outcome can be stunning.
That's the category into which we would place the work that mathematicians Jinyoung Park and Huy Tuan Pham did to prove the Kahn-Kalai Conjecture, which had been a major open problem in the field of probabilistic combinatorics. The press release announcing their proof describes how it connects to practical considerations:
The conjecture concerns determining the precise point (e.g. temperature, pressure, probability, etc.) at which a "phase transition" occurs in a large variety of systems. The systems are studied widely in statistical mechanics and graph theory. While this point is extremely hard to compute, in 2006 Jeff Kahn and Gil Kalai, past IAS Member (1995, 2000) and frequent visitor, conjectured that it is very close to another parameter which is much easier to compute. If true, it could be possible to approximate well when phase transitions occur. This has been called “the expectation threshold conjecture.’’
That's the sort of thing that would be very useful in applications like directing chemical reactions, managing an electrical grid, or determining the resilience of a financial system. What's more remarkable is that Park and Pham's proof is just a mere six pages long. If you're interested in finding out more, the invaluable Quanta Magazine introduces more information about their proof.
There is one more story that needs to be told under 2022's unofficial theme of persistence and dedication. That story is graduate student Jared Duker Lichtman's proof of a conjecture proposed by the prolific mathematician Paul Erdős regarding prime numbers and primitive sets. Fortunately for us, Lichtman discussed his proof with Numberphile's Brady Haran in the following video:
We've featured many Numberphile videos over the years, this one has quickly become one of our favorites. It's not the biggest math story of the year, but it's well worth your time in watching because it explores why the challenge of proving math conjectures can command such persistence and dedication!
Real Numbers Alone Cannot Describe Reality!
When we wrapped up the biggest stories in math for 2021, the publication of the paper by Marc-Olivier Renou, David Trillo, Mirjam Weilenmann, Thinh P. Le, Armin Tavakoli, Nicolas Gisin, Antonio Acín, and Miguel Navascués demonstration that a theory of quantum mechanics based only upon real numbers is false just barely missed our cutoff date for inclusion.
This is a massively important story with universal impact, because it means the universe itself cannot exist without complex numbers, or rather, a combination of both real numbers and imaginary numbers!
That's not just hyperbole coming from mathematicians. That's the direct outcome from two experiments that put real numbers to the test of explaining physical reality and found them wanting. Here's some background for the experiments:
Some physicists have attempted to build quantum theory using real numbers only, avoiding the imaginary realm with versions called “real quantum mechanics.” But without an experimental test of such theories, the question remained whether imaginary numbers were truly necessary in quantum physics, or just a useful computational tool.
A type of experiment known as a Bell test resolved a different quantum quandary, proving that quantum mechanics really requires strange quantum linkages between particles called entanglement. “We started thinking about whether an experiment of this sort could also refute real quantum mechanics,” says theoretical physicist Miguel Navascués of the Institute for Quantum Optics and Quantum Information Vienna. He and colleagues laid out a plan for an experiment in a paper posted online at arXiv.org in January 2021 and published December 15 in Nature.
In this plan, researchers would send pairs of entangled particles from two different sources to three different people, named according to conventional physics lingo as Alice, Bob and Charlie. Alice receives one particle, and can measure it using various settings that she chooses. Charlie does the same. Bob receives two particles and performs a special type of measurement to entangle the particles that Alice and Charlie receive. A real quantum theory, with no imaginary numbers, would predict different results than standard quantum physics, allowing the experiment to distinguish which one is correct.
Fan and colleagues performed such an experiment using photons, or particles of light, they report in a paper to be published in Physical Review Letters. By studying how Alice, Charlie and Bob’s results compare across many measurements, Fan, Navascués and colleagues show that the data could be described only by a quantum theory with complex numbers.
That wasn't the only experiment to suggest it takes both real and imaginary numbers to describe reality.
Another team of physicists conducted an experiment based on the same concept using a quantum computer made with superconductors, materials which conduct electricity without resistance. Those researchers, too, found that quantum physics requires complex numbers, they report in another paper to be published in Physical Review Letters. “We are curious about why complex numbers are necessary and play a fundamental role in quantum mechanics,” says quantum physicist Chao-Yang Lu of the University of Science and Technology of China in Hefei, a coauthor of the study.
The math of complex numbers is essential to the modern world, and is increasingly so with the development of advanced electronics and other technologies that are being built in the microscopic scales where quantum mechanics define what's possible. That central role makes the story of how real and imaginary numbers are essential for the universe's existence the Biggest Math Story of 2022. There just aren't any practical applications that are bigger than that!
Bonus Update: Physicist Sabine Hossenfelder discussed whether complex numbers exist back in March 2021, back when the paper was just a preprint! Here's the video:
Previously on Political Calculations
The Biggest Math Story of the Year is how we've traditionally marked the end of our posting year since 2014. Here are links to our previous editions and our coverage of other math stories during 2022:
- The Biggest Math Story of the Year (2014)
- The Biggest Math Story of 2015
- The Biggest Math Story of 2016
- The Biggest Math Story of 2017
- The Biggest Math Story of 2018
- The Biggest Math Story of 2019
- The Biggest Math Story of 2020
- The Biggest Math Story of 2021
- The Biggest Math Story of 2022
- The Invention of Imaginary Numbers
- The 37 Percent Solution
- The Oddness of Odd Numbers
- An Introduction to the Riemann Hypothesis
- Wordle for Maths
- How to Use a Measuring Tape to Assess Your Health Risk
- An Improved Method for Integrating Complex Equations
- The Binary Code Hidden Inside a Trick for Multiplying Numbers
- The Bungled Math Behind Biden's Failure to Approve Offshore Oil Permits
- The Math Inside the Magic
- How Long to Crack Your Password with Brute Force?
- Homer Simpson Is Made of Maths
- Words for Describing Probabilities
- Maxwell's Equations
- The Lurking Chaos in Ecosystems
- Are You Waking Up on the Right Side of the Bed?
- Maths Prove Slowly Rotating Black Holes Are Stable
- Can Statistics Catch a Cheater at Chess?
- The Dumbest Way to Solve a Maze
- A Mathematical Intersection Between Epidemiology and Chemistry
- What to Get a Maths Enthusiast for Christmas
This is Political Calculations' final post for 2022. Thank you for passing time with us this year - we hope you have a wonderful holiday season! We'll see you again in the New Year, which we'll start with another annual tradition by presenting a tool to help you find out what your paycheck will look like in 2023 after an increasingly cash-strapped U.S. government takes its cut from it....
Before we go, Quanta Magazine has put together an article and video with their take on the year's top three math breakthroughs, two of which will hopefully be familiar to you....
We'll see you in the new year!
What does the future hold for the quarterly dividends of the S&P 500 (Index: SPX) in 2023?
The answer to that question is visually presented in the following animated chart. As a bonus, we're also answering the question of how different the S&P 500's quarterly dividends for 2022 turned out with respect to what investors expected a year ago. Here's the chart:
In this chart, the data for past quarters reflects the final projection for dividends per share on the day the associated quarters' dividend futures contracts expired, which aligns with the actual amount of dividends paid during each contract's active period. The data for the projected quarters is that reported in the snapshots we took of the dividend futures data on 20 December 2021 and on 19 December 2022.
Looking at what was expected in 2022 versus what the index delivered, the animation reveals the year was more positive than had been expected by shareholders.
We also observe investors expected quarterly dividends to fall within a narrow range during 2022, ranging between a high of $16.02 per share in 2022-Q1 and a low of $15.76 per share in 2022-Q2. Investors also went into 2022 with the expectation that each quarter's dividend payout would be higher than the final dividends futures reported for 2021-Q4. Projected dividend payouts at the end of each dividend futures contract period ranged from a low of $16.53 per share in 2022-Q1 to a high of $17.00 per share in 2022-Q4. So quarterly dividends did indeed fall within a relatively narrow range, just one that was $0.75 to a little over $1.00 per share higher across the board than was projected before the year began.
Looking forward, investors at the end of 2022 are projecting a more negative future for the S&P 500's dividends during 2023. After peaking at a projected dividend payout of $17.25 per share at the expiration of 2023-Q1's dividend futures contract, investors expect dividend payouts to fall each quarter during 2023. The dividend payout for 2023-Q2 is projected to drop to $16.70 per share before falling more sharply in 2023-Q3 to $16.15 per share. 2023-Q4 would see the decline in quarterly dividend payouts decelerate to $16.05 per share.
Although we're not showing it in the animated chart, the S&P 500's projected dividends per share for 2024-Q1 is $16.25 per share. That figure is well below both the projection for 2023-Q1 and the final projection for 2022-Q1. The overall projected trend for S&P 500 dividends in 2023 is consistent with investor expectations of recessionary conditions during the year.
About the Dividend Futures Data
The dividend futures data we visualized in the animated chart is based on our records of the S&P 500's Quarterly Dividend Index Futures reported by the CME Group on 20 December 2021 and on 19 December 2022. This corresponds to the first Monday following the expiration of the respective years' fourth quarter's dividend futures contracts on the preceding Friday.
Dividend futures indicate the amount of dividends per share to be paid out over the period covered by each quarters dividend futures contracts, which start on the day after the preceding quarter's dividend futures contracts expire and end on the third Friday of the month ending the indicated quarter. So for example, as determined by dividend futures contracts, the now "current" quarter of 2023-Q1 began on Saturday, 17 December 2022 and will end on Friday, 16 March 2023.
That makes these figures different from the quarterly dividends per share figures reported by Standard and Poor, who reports the amount of dividends per share paid out during regular calendar quarters after the end of each quarter. This term mismatch accounts for the differences in dividends reported by both sources, with the biggest differences between the two typically seen in the first and fourth quarters of each year.
Since we're not mixing those results with the dividend futures data, the animated chart is providing an apples-to-apples comparison for the different snapshots in time of investor expectations.
Labels: dividends, forecasting, SP 500
Dividends by the Numbers is one of our most popular series. Each month, we discuss the U.S. stock market's metadata for the number of dividends that were declared, visualizing how many U.S. publicly-traded companies either increased or decreased their dividends, and report how many firms omitted paying dividends or resumed paying them and also the number of companies that announced they would pay an extra, or "special", dividend to their shareholding owners.
In doing that, we're following in the footsteps of legendary financial writer Bertie Forbes, who pioneered this kind of reporting in 1922. B.C. Forbes, a Scottish immigrant who founded the business and finance magazine that still bears his name today after becoming a U.S. citizen in 1917, was one of the earliest market observers to realize this data was telling an incredible story as the roaring twenties boom was getting underway. Within a year, he was incorporating the dividend metadata from several hundred stocks he regularly followed into his syndicated columns.
The 1920s was also when the Standard Statistics Company, the "Standard" in today's Standard and Poor, launched its market analytics business. The firm had its big breakthrough on 2 January 1929, when the Associated Press adopted its 90-stock composite index for its reporting on the U.S. stock market. The market capitalization weighted index is the direct precursor to the S&P 500, and the AP's decision played a large role in establishing the new index as widely reported market metric.
But that wasn't all the information that Standard Statistics compiled for the AP. They also compiled monthly dividend metadata as B.C. Forbes was doing, but for the entire U.S. stock market, which in that era consisted of more than 3,100 individual stocks.
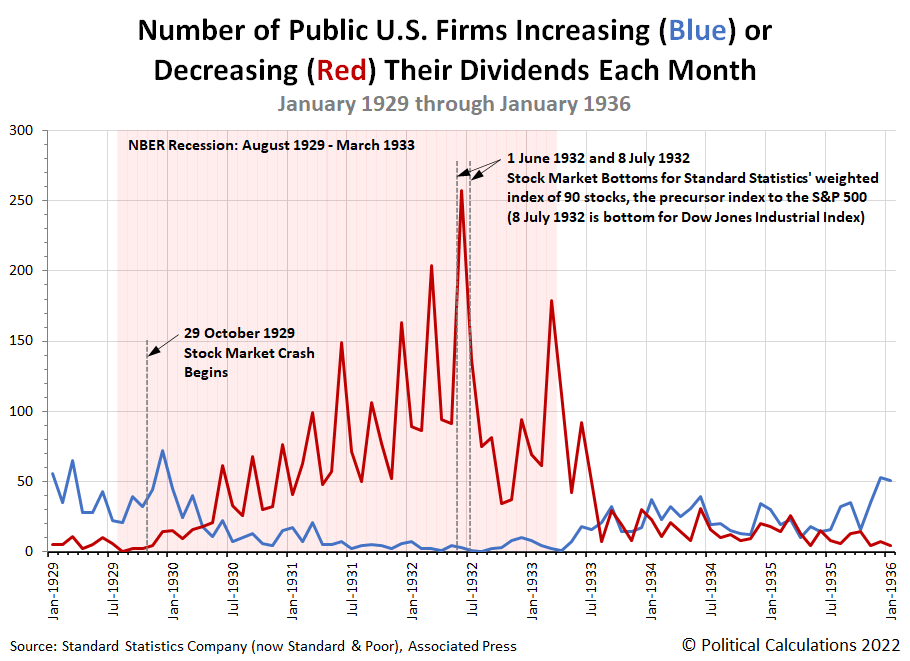
1929 is a remarkable year because it also marks the beginning of the Great Depression and the stock market crashes that signaled it was getting underway. The U.S. stock market's dividend metadata soon proved to be a vital indicator, particularly the number of dividend reductions that were announced each month. In the worst years of the depression, the reports changed to be presented on a weekly basis because the number of cuts had become so large.
We've reconstructed the data series for the number of dividend increases and reductions being announced each month from that era's contemporary news reporting. If you want to know what an economic disaster really looks like, here's the picture:
We selected this period to show the full cycle of dividend rises and reductions as started from their pre-Depression levels, to exploding in economic crisis, to once again resuming their pre-Depression levels.
We've also shown the period the National Bureau of Economic Research indicates the U.S. economy cycle went into and stayed in contraction after having peaked in August 1929. Note that the number of dividend cuts begins to rise above its pre-Depression levels some three-to-six months after the Depression started. After a year, there's a regular spike every three months as U.S. companies reported their earnings and as increasingly become the case, their dividend cuts. Those cuts kept getting worst until June 1932, when the number of dividend cuts peaked. That peak coincides with the market bottom for Standard Statistics' 90-stock composite index during the Great Depression.
Afterward, the number of dividend cuts reported each month began to fall as economic conditions improved. After the NBER-recession ended in March 1933, it took another three-to-six months for the number of dividend cuts to drop back to what we'll call "near pre-Depression levels". At the same time the number of dividend increases began to rise off the floor, also signaling the improvement taking place in the economy. But then it took another four years before dividend increases and decreases consistently tracked their pre-Depression levels.
After January 1936, reporting on dividend metadata became more sparse and eventually disappeared from regular news coverage. In the era since, it hasn't been a regular feature, even though its still reported each month by Standard Statistics successor firm, Standard and Poor. Only now, that metadata is included as part of a wider ranging report featuring much more market performance data, so it doesn't stand out the way it did when it was widely recognized as a vital market measure during the most critical period the U.S. economy has experienced.
At least, until several years ago, when we unknowingly followed in Bertie Forbes footsteps and brought it back to life as the main feature of a regular column. We only learned about Forbes' role in originating this kind of analysis because we went looking for historic metadata for dividends during the Great Depression and kept running into his syndicated columns as we reconstructed the data!
Labels: data visualization, dividends
Six Earth months, or rather, one Martian quarter has passed, which means it is time once again to estimate the red planet's gross domestic product!
As the Martian economy completes the third quarter for which we've estimated its planetary GDP, we find it is humming along after having run into a rough patch during the previous Martian quarter. Starting from Earthdate 7 July 2022, robotic mining operations have proceeded without significant technical interruption and the Perseverence rover has resumed collecting rock core samples. This activity followed nearly four Earth months with no sample collection when the rover traveled from the Octavia E. Butler Landing/Ch’ał outcrop where it drilled its previous core sample to the sample-rich geology of the Delta Front within the Jezero Crater.
The rover drilled nine samples during the Martian third quarter, with the samples placed into inventory pending their planned export to Earth. With a total of seventeen samples, we now have the following revised GDP estimates for Mars' first and second Martian quarters and an initial estimate for the third Martian quarter:
| Martian GDP Estimates (Constant 2021 U.S. Dollars) | |||
|---|---|---|---|
| Martian Quarter | First Quarter | Second Quarter | Third Quarter |
| Approximate Earthdates | 12 Jul 2021 - 31 Dec 2021 | 1 Jan 2022 - 21 Jun 2022 | 22 Jun 2022 - 11 Dec 2022 |
| Estimated GDP | $494,430 ($110,780 - $878,080) |
$296,658 ($66,468 - $526,848) |
$889,974 ($199,404 - $1,580,544) |
| Revision Level | Third | Second | Initial |
We estimate Mars' GDP tripled its previous quarter's revised GDP total during the planet's third quarter, falling just shy of $900,000 in terms of constant 2021 U.S. dollars. At present, we're valuing the two regolith samples collected by the Perseverance rover the same as the seven rock core samples it collected during the Martian third quarter in the absence of better valuation data for it. We're also assigning a minimal value to the Martian atmospheric sample the rover collected and stored during the Martian first quarter (in August 2021), given the very low density of the Martian atmosphere and the low premium of $50/gram given to Martian meteorites on Earth determined to have trapped atmospheric content within them.
Looking ahead to Mars' future export economy, NASA and the European Space Agency reached an agreement to establish a sample transfer depot at the Three Forks location within Mars' Jezero Crater. The Perseverence Rover will cache its full inventory of rock and atmospheric samples at the Three Forks Depot before their future export.
Unfortunately, the government space agencies have pushed back their planned export operations, with deliveries to Earth now delayed from 2030 to 2033. They've also changed their plans for how the samples will be recovered before their transportation to Earth:
... the Mars Sample Return campaign will no longer include the Sample Fetch Rover or its associated second lander. The Sample Retrieval Lander will include two sample recovery helicopters, based on the design of the Ingenuity helicopter, which has performed 29 flights at Mars and survived over a year beyond its original planned lifetime. The helicopters will provide a secondary capability to retrieve samples cached on the surface of Mars.
The ESA Earth Return Orbiter and its NASA-provided Capture, Containment, and Return System remain vital elements of the program architecture.
With planned launch dates for the Earth Return Orbiter and Sample Retrieval Lander in fall 2027 and summer 2028, respectively, the samples are expected to arrive on Earth in 2033.
The following three-minute video describes the final stage for how the samples will be delivered to Earth during the final stage of their transport.
Previously on Political Calculations
Labels: economics, ideas, technology
After a week that saw it rise as high as 4,019.65, the S&P 500 (Index: SPX) ultimately dropped 2.8% from where it ended the previous week to close at 3,852.36 on Friday, 16 December 2022.
Here's the latest update to the dividend futures-based model's alternature futures chart:
Before we go any further, let's recap a short bit of our analysis from last week, which will help explain what's going on in the updated portion of the alternative futures chart:
If investors focus predominantly on 2023-Q1, the trajectory of the S&P 500 will remain within the redzone forecast range. If investors shift a larger portion of their attention further forward in time to 2023-Q2, the trajectory will drop below this indicated range.
On Wednesday, 14 December 2022, the trajectory of the S&P 500 has risen to the middle portion of the redzone forecast range, corresponding with investors mostly focusing their forward-looking attention on 2023-Q1. But that focus was very short-lived, as investors quickly shifted their forward-looking attention beyond the first quarter of 2023.
Here's what changed to prompt that shift in how far forward investors are looking. After the Fed's expected half point rate hike on 14 December 2022, news indicating developing weakness for the U.S. economy reshaped investors expectations of how the Fed will be changing interest rates in 2023. Those changes are captured by the CME Group's FedWatch Tool, which dialed back its forecast for the Fed's next rate hike from a half point to just a quarter point at its 1 February (2023-Q1) meeting. The FedWatch tool then sees just one more quarter point rate hike in March (2023-Q1), where the Federal Funds Rate would top out in the 4.75-5.00% range, below what they expected just a week earlier. Looking further forward, developing expectations for a recession in 2023 have the FedWatch tool projecting two quarter point rate cuts, the first in September (2023-Q3) and the second in December (2023-Q4).
Based on this information, through Friday, 16 December 2022, we would describe the level of the S&P 500 as consistent with investors splitting their attention between 2023-Q1 and 2023-Q3. That level is coincidentally near the middle of where we might sketch a new redzone forecast range on the chart to indicate where the S&P 500 would be if investors were closely focused on 2023-Q2.
Here are the week's market-moving headlines:
- Monday, 12 December 2022
- Signs and portents for the U.S. economy:
- Oil up $2/bbl on supply risks amid ongoing Keystone outage
- Americans expected waning inflation pressures, rising incomes in November
- Investors don't have high opinion of Fed minions' abilities:
- Wall St climbs with inflation, Fed on deck
- Tuesday, 13 December 2022
- Signs and portents for the U.S. economy:
- Nov U.S. CPI cools down, spelling relief for markets
- U.S. consumer prices increase moderately in November
- Food inflation: Tight grain, oilseed supplies to keep prices elevated
- U.S. existing-home sales to slide to 11-year low in 2023, NAR says
- Fed seen slowing rate hikes, likely ending them below 5%
- Bigger stimulus developing in China:
- Wall St rises after CPI data but Fed concerns persist
- Wednesday, 14 December 2022
- Signs and portents for the U.S. economy:
- U.S. consumer loan delinquencies seen surging to 13-year high in 2023 - study
- U.S. import prices drop further; inflation pressures easing
- Fed raises rates by half percentage point, sees economy nearing stall speed
- Fed hikes rates by 50 bp, as expected, keeps hawkish tone
- Fed policymakers see interest rates higher, for longer
- Fed's Powell says inflation data received in Oct and Nov shows 'welcome reduction'
- Bigger trouble developing in Japan, Brazil:
- Japan manufacturers' mood sour as cost pressures bite, service sector upbeat
- Brazil's economic activity shrinks in October on rate hike impact
- Smaller trouble developing in the Eurozone?
- Even bigger stimulus developing in China:
- Central bank rate hikes to continue through end of 2022:
- ECB minions say elevated inflation to stay in Eurozone for another three years:
- Wall Street ends lower after latest Fed rate hike
- Thursday, 15 December 2022
- Signs and portents for the U.S. economy:
- U.S. retail sales post biggest drop in 11 months; labor market tight
- U.S. manufacturing output dragged down by motor vehicle weakness
- Bigger trouble developing in China, Eurozone:
- China's factory, retail sectors skid as COVID hits growth
- China property slumps further in Nov, policies support gradual recovery
- French economy forecast to contract before recovering next year
- BOJ minions say they can't stop, won't stop never-ending stimulus:
- Central bank minions signal more rate hikes are comint, start to signal rate hikes will slow, end in 2023:
- Bank of England raises rates to 3.5%, sees more hikes ahead
- Norway central bank hikes rate by quarter point, likely to act again
- Swiss National Bank says inflation battle not yet won
- Taiwan central bank signals end to rate hikes next year
- Bank of Mexico hikes rate to 10.50%, signals another increase coming
- ECB minions delivers half point rate hike into developing Eurozone recession:
- ECB raises rates again, outlines balance sheet run off
- ECB slows rate hikes but pledges more to keep up inflation fight
- ECB's Lagarde offers back-to-back rate hikes to woo dissenters
- ECB to start offloading bond holdings in March
- ECB raises inflation, cuts 2023 growth projection
- Wall Street slumps as Fed heightens recession fears
- Friday, 16 December 2022
- Signs and portents for the U.S. economy:
- Fed minions claim they won't start rate cuts until after 2023 recession is well underway:
- Bigger stimulus developing in China:
- China's economy picking up but "arduous efforts" needed to sustain momentum - state planner
- China says it will step up support for economy in 2023 amid COVID pains
- Bigger trouble developing in Japan:
- Japan Dec factory activity contracts at fastest pace in 26 months
- Japan Nov consumer inflation likely to hit fresh four-decade high - Reuters poll
- BOJ minions thinking about ending never-ending stimulus:
- Bigger trouble in the Eurozone not as bad as expected:
- ECB minions say they won't stop fighting inflation, say their jawboning is just like a rate hike, say they won't have more big rate hikes:
- ECB's Villeroy: Match against inflation is not over
- Strong ECB statement equivalent to a bigger rate hike, Holzmann says
- ECB's Centeno sees very low probability of more 75 bps rate hikes
- ECB’s Knot says Fed is closer to end of rate hikes than ECB
- Wall Street's slump continues as recession fears mount
The Atlanta Fed's GDPNow tool's projection for real GDP growth in the current quarter of 2022-Q4 dropped back to +2.8% from last week's +3.2% estimate. The "Blue Chip consensus" still projects over 1% real economic growth for the current quarter of 2022-Q4.
This is the last post in our S&P 500 chaos series for 2022. We'll be back in the first week of Janaury 2023 to recap the final two trading weeks of 2022, where the big question we have going into those final weeks is whether there will be one or two more Lévy flight events to end the volatile year of trading.
It's that time of year once again! Families are already focusing on the details of decorating to celebrate Christmas, and how to decorate their Christmas tree in particular.
As you hang your family's ornaments this year, you've probably noticed most of them aren't very exciting. And to be sure, they're not. If you think about it, their only function is to hang there on your tree. Wouldn't it be nice to have Christmas ornaments that feature a lot more action to liven the holiday spirit up.
Inventors Marc Segan and Michael Newsome were thinking along those lines back in the early 1990s. Their idea was to transform a large section of a Christmas tree into Santa's ski resort, complete with a ski run and lift, where a miniature figure could ride the lift up to the top, then slalom through the branches and around the tree back to the bottom before repeating the cycle. For their innovative thinking, they were awarded U.S. Patent 5,279,871 on 18 January 1994. Here's Figure 1 from the patent, which we've colorized to make the various components stand out:
Segan and Newsome describe how they brought action to holiday ornaments with their invention:
The present invention is a Christmas display resembling a ski-lift and ski-slope, for use in conjunction with a Christmas tree. The display comprises a track having a first end and a second end, wherein the first end is at a higher elevation than the second end, and a lift disposed between the first end and the second end. The device also comprises a plurality of figurines having a base configured for slidable movement along track from the first end of track to the second end of track whereby the lift transports the figurine back to the first end of the track in a continuous manner.
The figurine (30) in the patent illustration is a miniature Santa on skis! Just imagine him skiing around your tree through the whole holiday season, celebrating the holiday at the ski resort on your Christmas tree. The only way you could have more action in a Christmas setting with with a scale model of the Nakatomi Plaza building and a miniature reenactment of Die Hard.
From the Inventions in Everything Archives
Here's a selection of Christmas and tree-related inventions the IIE team has previously featured:
Labels: technology
After cooling in October 2022, Earth's economy picked up somewhat in November 2022. That rebound however hasn't risen above the recent peak set at the end of 2022-Q3.
That's the latest assessment of the state of the world's economy as measured on the side of an erupting volcano in Hawaii. More specifically, the Mauna Loa Observatory's measurements of the changing concentration of carbon dioxide in the Earth's atmosphere that are linked to human activities give us the following picture through November 2022.
With the Mauna Loa volcano erupting, we wondered what kind of impact that might have on the observatory's measurements of atmospheric carbon dioxide. According to the observatory, there's very little-to-none, because they can easily account for it:
Most of the time, the observatory experiences “baseline” conditions and measures clean air which has been over the Pacific Ocean for days or weeks. We know this because the CO2 analyzer usually gives a very steady reading which varies by less than 3/10 of a part per million (ppm) from hour to hour. These are the conditions we use to calculate the monthly averages that go into the famous 50-year graph of atmospheric CO2 concentration.
We only detect volcanic CO2 from the Mauna Loa summit late at night at times when the regional winds are light and southerly. Under these conditions, a temperature inversion forms above the ground, and the volcanic emissions are trapped near the surface and travel down our side of the mountain slope. When the volcanic emissions arrive at the observatory, the CO2 analyzer readings increase by several parts per million, and the measured amounts become highly variable for periods of several minutes to a few hours. In the last decade, this has occurred on about 15% of nights between midnight and 6 a.m.
These periods of elevated and variable CO2 levels are so different from the typical measurements that is easy to remove them from the final data set using a simple mathematical “filter.”
NOAA’s Earth Science Research Laboratory program also measures CO2 in weekly flask samples taken at over 60 remote locations around the world. The Mauna Loa Observatory baseline CO2 concentrations agree very well with flask measurements taken at a similar latitude around the world, which confirms that the volcanic CO2 does not affect our final results.
We use those final results in our methodology for evaluating the relative health of the global economy, which means our assessment isn't affected by the erupting volcano just around the corner from where those CO₂ measurements are taken.
Speaking of which, here is livestream from the U.S. Geological Survey's web cam set up to monitor the eruption, which lets us close with the closest we can get to a bang for what's otherwise pretty dry analysis....
The USGS reports they've been having intermittent problems with the livestream, so you may be seeing a static video that was recorded shortly before the connection was dropped. It's always a pain to get signal bars out in the middle of nowhere.
References
National Oceanographic and Atmospheric Administration. Earth System Research Laboratory. Mauna Loa Observatory CO2 Data. [Text File]. Updated 5 December 2022. Accessed 5 December 2022.
Labels: environment
Data for October 2022 indicates the total value of goods being imported by the U.S. from China shrank year-over-year, pointing to developing weakness in the relative health of the U.S. economy. At the same time, the value of U.S. exports to China was up, but has dropped to single digit growth rates after hovering at a 20% year-over-year growth rate in both August and September 2022.
The following chart shows how these new developments fit into the modern history of trade between the two nations.
The shrinkage in the value of goods imported from China was more than enough to offset the slowed growth in U.S. exports to China, pulling the combined value of trade between the two countries down. The next chart illustrates that change has pulled the trajectory of trade down after having briefly outperformed a post-pandemic trade recovery counterfactual.
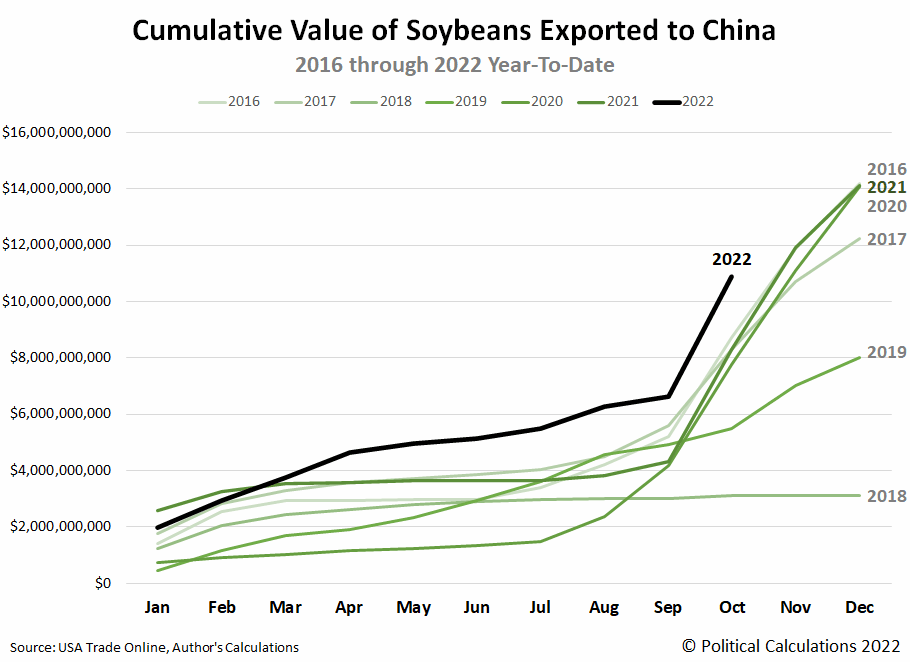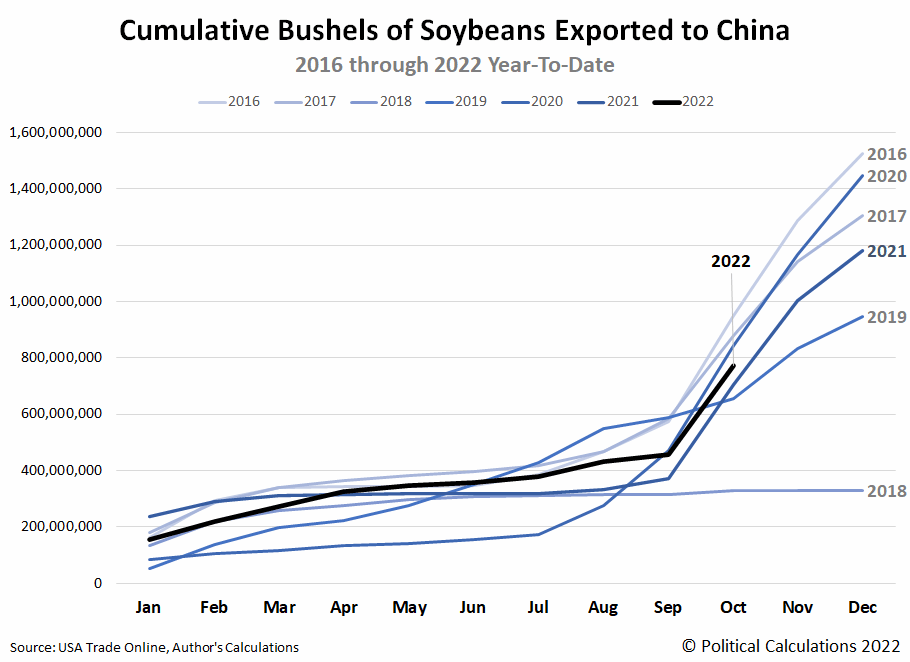
The primary reason U.S. exports to China were positive in October 2022 is because of the inflation of soybean prices. Combined with having entered peak soybean export season, the cumulative value of soybean exports is setting records, although the cumulative quantity of soybeans exported is significantly below recent years. The following animated chart cycles between both sets of data, pay attention to 2022's levels for both.
At 2021's prices, we estimate the real value of 2022's U.S. soybean exports to China is running about 12% below 2021's levels.
References
U.S. Census Bureau. Trade in Goods with China. Last updated: 3 November 2022.
U.S. Department of Agriculture. Soybeans - Price Received, Measured in $/bushel. [Online Database]. Accessed 10 December 2022.
U.S. Trade Online. Soybean Exports to China. [Online Database]. Accessed: 10 December 2022.
Labels: trade
Welcome to the blogosphere's toolchest! Here, unlike other blogs dedicated to analyzing current events, we create easy-to-use, simple tools to do the math related to them so you can get in on the action too! If you would like to learn more about these tools, or if you would like to contribute ideas to develop for this blog, please e-mail us at:
ironman at politicalcalculations
Thanks in advance!
Closing values for previous trading day.
This site is primarily powered by:
CSS Validation
RSS Site Feed
JavaScript
The tools on this site are built using JavaScript. If you would like to learn more, one of the best free resources on the web is available at W3Schools.com.