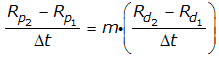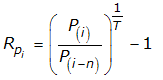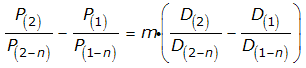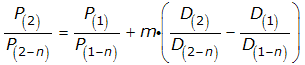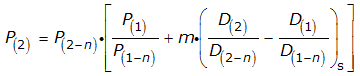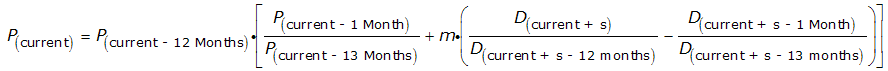Changes in stock prices are largely driven by changes in the expected future growth rate of their corresponding trailing year dividends per share. Today, we're going to show you how that works, with math. You've been warned - if you don't want to deal with math, now's the time to bail out!
Seriously. We'll be using a lot of algebra. This is your last chance....
Still here? Alright then, let's get started....
The basic relationship we've observed that exists between changes in the rate of growth of stock prices and changes in the rate of growth of their dividends per share, or in our terminology, their accelerations, is given by the equation:
Where Ap is the change in the rate of growth of stock prices and Ad is the change in the rate of growth of dividends per share. m is an amplification factor that varies over long periods of time but can be nearly constant for short-to-intermediate periods of time, which we'll focus more upon in future posts.
As we've formulated it, these accelerations represent the change in the compound annual growth rate of stock prices (Rp) and trailing year dividends per share (Rd) between two points in time (Δt):
Substituting these expressions back into our basic relationship gives the following:
Multiplying each term on both sides of the equation by the time interval (Δt), we are able to eliminate this term altogether:
We can now replace the compound annual growth rates with their corresponding stock price and trailing year dividend per share data. The generic compound annualized growth rate of both stock prices (Rp) and trailing year dividends per share (Rd) are given by the following equations:
For these equations, i represents the more recent data, while i-n indicates an older data point, occurring some n periods or time before i. Substituting these terms into our equation relating the compound annual growth rates of stock prices and trailing year dividends per share leads to the following equation:
Combining like terms, we can simplify the equation:
We'll next simplify the equation further by letting T equal 1 period of time. This allows us to eliminate the exponents, but also requires that we set the time interval between (i) and (i-n) to span the same time interval. We get the following equation:
Our next step will be to solve for P(2), the most recent stock price. First adding P(1)/P(1-n) to both sides of the equation:
We'll finally solve for the most recent stock price by multiplying each term in the equation by P(2-n):
But wait, that's not all! Since changes in stock prices are largely driven by changes in the expected future growth rate of their corresponding trailing year dividends per share, we need to account for the fact that investors are looking ahead in time. We'll do this by indicating that the dividend data is shifted ahead some period of time, s:
Now, how would we use this equation in practice? Let's say that our stock price data consists of the average daily closing value of the S&P 500 and the index' corresponding trailing year dividends per share for each month since January 1871. If we use year-over-year data for our calculations (T equal to one year), we might calculate the average monthly stock price for any month beginning with February 1872 as follows (click the image for a larger, more readable version):
Here, the subscripts indicate the relationship of the data point to the month for which we're trying to solve, which we've identified as "Current". Subtracting a given number from this figure indicates that the data point is that many months before the current month. Adding a given number to this figure indicates that the data point is that many months in the future from the current month.
In this equation, we're left with two unknowns in being able to anticipate where stock prices will be set: our amplification factor (m), and our forward looking time shift (s), which itself varies with time. Both of which might be determined in practice by observation and trial and error. We should also point out that the variations in these two factors are specifically what makes the stock market a chaotic place.
And if you can get your hands on dividend futures data, you might reasonably predict how stock prices today will adapt to changes in how fast investors expect dividends to grow in the future.
There's a tool in here somewhere....
Update 28 April 2009: Based on some really good feedback from a really sharp reader, we've altered the images for the second, third and fourth equations (click links for originals) presented in this post, changing "dt" to "Δt", to better clarify that we're not necessarily looking at infinitesimal units of time, but rather discrete intervals of time!
Elsewhere on Political Calculations
| Essential Reading to Get Up to Speed with Us! |
|---|
| Date Posted | Post | Remark |
|---|---|---|
| 2007-12-06 | The Sun, in the Center | We used historic data for the S&P 500 to uncover the fundamental power-law relationship that exists between dividends per share and stock prices. Our third anniversary post! |
| 2008-12-10 | Acceleration, Amplification and Shifting Time | We introduce evidence demonstrating that the breakdown in stock prices beginning in January 2008 was a very orderly process. Our fourth anniversary post, and the grandfather to this one! |
| 2007-12-17 | Deriving the Price Dividend Growth Ratio | We do hard core algebra to identify what makes up the different parts of the fundamental relationship between stock prices and dividends. And a mind control experiment (we know better than to post raw math by itself in a blog post!) |
| 2008-06-24 | Stock Prices: Normal Until They're Not, But They're Not Normal! | If you've read enough of our posts, you'll note that we've often presented our data using something that looks a lot like control charts as a tool to identify significant changes in stock prices with respect to their underlying dividends per share. This post explains why! |
| 2009-02-19 | Evidence of Order Underlying Chaos in the Stock Market | You wouldn't think it to look at it, but chaos in the stock market isn't necessarily a bad thing, at least, once you have the tools to sort it out.... |
| 2009-01-28 | Unraveling Chaos | We follow up our groundbreaking fourth anniversary post by first introducing the basic relationship between the acceleration of stock prices and trailing year dividends per share. |
| 2008-08-25 | The S&P 500 from December 1991 Onward | This is the first post in which we noted that changes in the rate of growth of the S&P 500's dividends are correlated with and perhaps even drive larger changes in stock prices. |
| 2008-11-19 | The Black Monday Stock Market Crash, Explained | We identify changes in the acceleration of the growth of dividends as a key factor driving changes in stock prices. We'll be taking a closer look at this event again sometime in the future, as we were rather stunned to see the correlations apparent in the data since 2001, which we presented in this post. |
| 2008-08-28 | Hey Look - Brownian Motion! | This post looks at the Dot-com Bubble, in which stock prices and dividends per share were fully decoupled from each other, which we should note would make the kind of analysis presented in this post unworkable until the relationship is re-established. The result: unadulterated Brownian Motion (complete with video!) |
| 2008-07-15 | Defining Bubbles, Order, Disorder and Disruptive Events | We provide our operating definitions for each of these concepts describing the associated states of the stock market. |
| 2008-03-18 | Recognizing Disorder in the Stock Market | How do you know when how things were aren't the way they're going to be with stocks? We discuss how to recognize when disorder erupts in the stock market. |
| 2008-06-12 | Emerging Order in the Stock Market | The flip side to our post on how to recognize when disorder has erupted in the stock market. Plus, we introduce quantum phenonoma! |
| 2008-01-23 | Distress, Recessions, Market Bottoms and the Future | We find an interesting correlation between when the market hits bottom, recessions and peaks of distress as measured by our price-dividend growth rate ratio! |
| 2008-01-09 | The Beating Heart of the Stock Market | Here, we find we can use the price-dividend growth rate ratio as a tool to measure the level of distress in the stock market. |
| 2006-12-06 | The S&P 500 at Your Fingertips | We put the entire history of the S&P 500, including the index' price, dividends, and earnings data at your fingertips! As a bonus, we also find the rate of return between any two calendar months in the index' history, both with and without inflation and with and without dividend reinvestment! |
Image Credit: Wired
Labels: chaos, dividends, forecasting, stock market
- posted by Ironman at 11:15 AM | Permalink | |
