No, this post is not about Freakonomics, even though we've borrowed the cover art! Instead, we're referring to the challenge of comparing income data by age group for the years 1995 and 2005.

Just how do you compare the income data, and the 10 years worth of change between them, for the two years of our interest?

It's a bit like comparing apples and oranges. Inside a paper bag, they might be superficially similar (size, shape, weight, etc.), but outside the bag, they're so distinct from one another that no one would ever mistake one for the other.

The income data we've been looking at for 1995 and 2005 is a lot like that. To make a solid comparison between these two years, we need to change one of them from an apple into a much more directly comparable orange. This post is about how we've done it.

Factoring in Inflation

We started by taking the monetary figures within the 1995 data and simply adjusting them for inflation. Since our 2005 data is presented in 2004 U.S. dollars, and likewise, the 1995 data is presented in 1994 U.S. dollars, our first adjustment was to convert the 1995 data to constant 2004 U.S. dollars.

We did this using Oregon State's Robert Sahr's inflation conversion factors for 2004 U.S. dollars (available in this PDF document), which provides the means for converting the value of U.S. dollars in any year from 1800 through the current year as well as projections out to 2015 into 2004 U.S. dollars!

Essentially, using these factors, we recognized that thanks to inflation, a 2004 U.S. dollar is worth just 78.5% of the value of a 1994 U.S. dollar. So, we divided each monetary figure in the 1995 data by the conversion factor of 0.785 to obtain its 2004 equivalent!

Distributions R Us

Doing that created a new problem. Instead of having directly comparable income ranges between the two years, we were left with comparing the ranges that didn't exactly match up. For instance, the lowest income range for 2005 is $1 - $2,499, while our inflation converted data for 1994 had changed from these figures in 1994 U.S. dollars to be $1.27 - $3,183.44 in 2004 U.S. dollars! While it's nice that they're all in the same valued money terms, it would be really great if we could directly compare the ranges.

What we needed was something like a distribution that would allow us to directly match up the data for both years in 2004 U.S. dollars. So, we created a distribution for each year. Going back to the original data for each year, we recognized that each income range in the Current Population Survey's income data really represents two things.

First, the obvious - it provides the number of persons in each age group who have annual income within the indicated range. Next, the not-so-obvious - if we progressively add up all the people in each of the individual age ranges, it provides the number of persons who earn the income at the top of the indicated income range, or less.

So, for instance, if we look at the 2005 data for the Age 15-24 group and look at the first two income ranges, we find that 6,059,000 persons within this group had annual income with the range of $1-$2,499 and that 3,432,000 persons earned income within the next higher level of $2,500-$4,999.

But, if we progressively add the persons in the higher level to the lower level, we obtain a distribution that tells us that there are 6,059,000 persons earning up to $2,499, and that there are 9,491,000 persons earning $4,999 or less. And so on all the way up to the top income level in the report of $95,000.

We can then take this data and create a mathematical representation of it. We observed that the raw data points seems to follow a sigmoidal distribution, so we used ZunZun's online 2-D curve-fitting tools to create formulas to represent each set of our data (one for each age group in both 1995 and 2005.) Our sigmoid functions follow the basic form:

Where a, b, c and d are unique values for each age group, e is a mathematical constant, Income is a given annual income amount and the Number of Individuals is that for those who make a given annual income, or less. We can find the number of individuals in a given income range by subtracting the value obtained using the lower income level from the value obtained using the higher one.

The chart below represents our effort for the 1995 data, converted to constant 2004 U.S. dollars:

And here's our chart for the 2005 data, for which we followed the same procedure, omitting only the inflation adjustment since it's already expressed in 2004 U.S. dollars:

We can now directly compare income data from 1995 and 2005, at any income level from $0 to $95,000 in constant 2004 U.S. dollars.

The Next Level

The other cool thing about now having this data being described by mathematical functions is that we can now precisely calculate the total amount of income earned by all individuals within the various age groups for a given income range by integrating our formula above, which we obtained using Wolfram's Integrator:

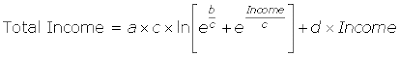
We can now find the total income earned for each age group between any two income levels by subtracting the value obtained in this formula from the lower income level from that obtained using the higher income level.

What's Wrong with What We've Done?

Our distribution for the Number of Individuals of each age group is really good, except at the low end of the income spectrum. This problem arises from the lack of good data here, primarily due to how the Current Population Survey actually grouped people at the lowest end of the annual income earning level.

While we've made frequent reference to the $1-2,499 income range, the raw data for this range also includes those who earned less: either those who earned no income (such as Will Smith's character in The Pursuit of Happyness, congressional pages, unpaid interns, and generally anybody trading income for experience or networking contacts) and those who worked but had a net loss (budding entrepreneurs getting their businesses off the ground, etc.)

The problem with that is we don't know how many people fall into those groups, since they fall in with the part-timers who predominate in this lowest annual income range. So, we set our curve-fitting distribution data at 0 individuals at $0 annual income.

Because of that, our modeled distribution curve has the greatest error from the actual data we had to work with at this lowest end of the income spectrum. The good news is that our distributions become better (low errors compared to actual data figures) at annual income levels above $7,500 (off by less than 3%), and get better and better as the income levels increase.

What's Next

A lot of analysis, followed by a bit of mythbusting, and along the way, some new tools (this is Political Calculations, after all!) Stay tuned….

Labels: income, income distribution, math

- posted by Ironman at 10:46 PM | Permalink | Home |