We've come to the end of 2023, making it time to take stock of the biggest math stories of the year that was!

In choosing these stories, we've emphasized math stories involving practical applications in selecting the Biggest Math Story of 2023, which we'll present at the end of this year's edition after going through the runners-up.

That's not to say that we don't find other big, pure math stories impressive. For example, 2023 saw both a proof for a nearly-100-year old problem in Ramsey theory and the discovery of the ninth Dedekind number, 286,386,577,668,298,411,128,469,151,667,598,498,812,366, which is also an achievement in computing.

But these aren't examples of the kinds of stories with great potential to affect people's lives or explain the world in which we live. That's what separates practical math from pure math. And as we go through the runners-up before reaching the Biggest Math Story of 2023, what stands out is the connections between the pure and the practical. It's a true bonus whenever there's also fun to be had with that math.

It all starts now! Let's begin with a unusually big story that surprisingly didn't much attention during the year.

An Unexpected Link Between Number Theory and Evolutionary Genetics

The biggest math story of 2022 was the discovery that complex numbers, combining real and imaginary components, are essential for the existence of the universe. As practical applications go, it doesn't get much bigger than the universe. This story is a good place to start the 2023 edition of our year-ending series, because it points to a connection between mathematics and biology that potentially affects all life within the universe!

A team of researchers identified a potential application of number theory for explaining some vital characteristics of robustness observed in evolutionary genetics. What makes their findings special is that number theory in mathematics is often limited to applications that are themselves highly math dependent, such as computer coding or modern cryptography. Since evolutionary genetics is inherent to biology, finding a linkage between number theory concept and biology was unexpected.

From here, we'll turn to the University of Oxford's press release because it describes their discovery in layman's terms:

... the team of researchers (from Oxford, Harvard, Cambridge, GUST, MIT, Imperial, and the Alan Turing Institute) have discovered a deep connection between the sums-of-digits function from number theory and a key quantity in genetics, the phenotype mutational robustness. This quality is defined as the average probability that a point mutation does not change a phenotype (a characteristic of an organism).

The discovery may have important implications for evolutionary genetics. Many genetic mutations are neutral, meaning that they can slowly accumulate over time without affecting the viability of the phenotype. These neutral mutations cause genome sequences to change at a steady rate over time. Because this rate is known, scientists can compare the percentage difference in the sequence between two organisms and infer when their latest common ancestor lived.

But the existence of these neutral mutations posed an important question: what fraction of mutations to a sequence are neutral? This property, called the phenotype mutational robustness, defines the average amount of mutations that can occur across all sequences without affecting the phenotype.

Professor Ard Louis from the University of Oxford, who led the study, said, "We have known for some time that many biological systems exhibit remarkably high phenotype robustness, without which evolution would not be possible. But we didn't know what the absolute maximal robustness possible would be, or if there even was a maximum."

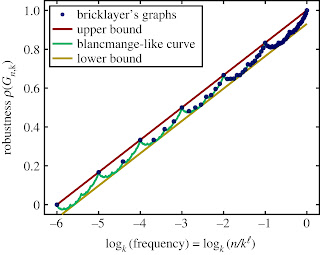
It is precisely this question that the team has answered. They proved that the maximum robustness is proportional to the logarithm of the fraction of all possible sequences that map to a phenotype, with a correction which is given by the sums of digits function sk(n), defined as the sum of the digits of a natural number n in base k. For example, for n = 123 in base 10, the digit sum would be s10(123) = 1 + 2 + 3 = 6.

Another surprise was that the maximum robustness also turns out to be related to the famous Tagaki function, a bizarre function that is continuous everywhere, but differentiable nowhere. This fractal function is also called the blancmange curve, because it looks like the French dessert.

First author Dr. Vaibhav Mohanty (Harvard Medical School) added, "What is most surprising is that we found clear evidence in the mapping from sequences to RNA secondary structures that nature in some cases achieves the exact maximum robustness bound. It's as if biology knows about the fractal sums-of-digits function."

A blancmange is a fancy molded gelatin dessert, whose defining feature is its scalloped or wave-like sides. The green curve in this section's illustration is the contour the authors are attempting describe.

Its still early days for this new application however, which keeps this math story from being the biggest of the year.

Buying a Winning Lottery Ticket

Our next contender for the biggest math story of the year involves the maths of probability and statistics, with the side benefit of potentially helping you win money in playing the lottery. Which if you can make it work for you, could be a very practical application!

Starting with the prospect of improving your chances of getting a winning ticket in the lottery, University of Manchester mathematicians studied the United Kingdom's national lottery, in which players choose 6 of 59 possible numbers that might be drawn when numbers are randomly selected. They applied graph theory to determine the minimum number of tickets lottery players would have to buy to get at least one that would win in each drawing.

We should note a "winning ticket" means a ticket that wins any of the possible payouts for the U.K.'s national lottery, not the 'Lotto' jackpot that's the main attraction to players. The University of Manchester's press release describes what they did to find how many tickets they needed to get any payback at all:

Focusing on the National Lottery’s flagship game ‘Lotto’, which draws six random numbers from 1 to 59, Dr David Stewart and Dr David Cushing found that 27 is the lowest possible number of tickets needed to guarantee a win – although, importantly, with no guarantee of a profit.

They describe the solution using a mathematical system called finite geometry, which centres around a triangle-like structure called a Fano plane. Each point of the structure is plotted with pairs of numbers and connected with lines – each line generates a set of six numbers, which equates to one ticket.

It takes three Fano planes and two triangles to cover all 59 numbers and generate 27 sets of tickets.

Choosing tickets in this way guarantees that no matter which of the 45,057,474 possible draws occurs, at least one of the tickets will have at least two numbers in common. From any draw of six, two numbers must appear on one of the five geometric structures, which ensures they appear on at least one ticket.

But Dr Stewart and Dr Cushing say that the hard work is actually showing that achieving the same outcome with 26 tickets is not possible.

The researchers note that buying 27 lottery tickets for the U.K.'s Lotto game will cost players £54. They indicate players will never make back that stake in "almost 99% of cases".

Getting Better Odds to Win a Coin Flip

Researchers at the University of Amsterdam found a trick that could give you a small edge in beating the odds of winning coin tosses. The trick is to see which side of the coin is originally facing up when it is tossed. If you can, there's a 50.8% chances that same side will be the the winner of the coin toss!

Although the same-side bias odds are close to even, it's also enough of a bias that coin flip odds are skewed as much as some casino games are in favoring the house. Here's how corresponding author František Bartoš described it:

If you bet a dollar on the outcome of a coin toss 1000 times, knowing the starting position of the coin toss would earn you 19$ on average. This is more than the casino advantage for 6deck blackjack against an optimal player (5$) but less than that for single-zero roulette (27$).

— František Bartoš (@BartosFra) October 9, 2023

Fortunes have been made by casino operators with those kind of biased odds in their favor.

Meanwhile, we built a tool to simulate a biased coin toss, assuming that the side you see up is always "Heads". By all means, take it for a test drive to see if you can put it to your own practical application!

Artificial Intelligence Speeds Math Proofs

2021 was the year artificial intelligence qualified as the biggest math story of the year. 2023 has seen an acceleration of AI systems capable of generating images and writing, but AI in the form of proof assistants also made a mark in advancing mathmatics.

That's the most practical application part of the story of how a team of four mathematicians proved Kati Marton's conjecture, considered by many mathematicians to be the "holy grail" of combinatorics. The invaluable Quanta Magazine covered the story of how the formalization of their proof came together:

Eventually, the group pushed through, and on November 9, they posted their paper. They proved that if A + A is no bigger than k times the size of A, then A can be covered by no more than about k¹² shifts of a subgroup that is no bigger than A. This is a potentially enormous number of shifts. But it is a polynomial, so it doesn’t grow exponentially faster as k gets bigger, as it would if k were in the exponent.

A few days later, Tao began to formalize the proof. He ran the formalization project collaboratively, using the version-control package GitHub to coordinate contributions from 25 volunteers around the world. They used a tool called Blueprint developed by Patrick Massot, a mathematician at Paris-Saclay University, to organize the efforts to translate from what Tao called “Mathematical English” into computer code. Blueprint can, among other things, create a chart depicting the various logical steps involved in the proof. Once all the bubbles were covered in what Tao called a “lovely shade of green,” the team was done. They discovered a few very minor typos in the paper — in an online message, Tao noted that “the most mathematically interesting portions of the project were relatively straightforward to formalize, but it was the technical ‘obvious’ steps that took the longest.”

The increasing usefulness of computer-assisted automation tools continued to be one of the biggest math stories of 2023, but not the biggest.

A Unique Tile Makes a Pattern That Never Repeats

It was two breakthrough discoveries in the ancient mathematical field of geometry, of all things, that made for the biggest math story of 2023! March had the first part of the story of the invention of an unusually-shaped einstein ("one-stone") tile, whose pattern would never repeat nor leave any gaps when tiled over a plane.

While that marked an improvement over Roger Penrose's aperiodic tiling, which requires two differently shaped tiles to accomplish the same feat, geometers had still never managed to find one tile shape that would do the same thing.

And in truth, they still hadn't, because the einstein "hat" tile required some tiles to be flipped over to fully "tile the plane", as they say in geometry. If you try doing that with common bathroom tiles, you'll quickly see that something is off with that approach.

In June, the same team tweaked their previous concept and created the "Spectre" tile and completed the solution to the centuries-old challenge.

It's only been months, but the new einstein and Spectre tiles are already making their presence felt in the real world. You can buy a T-shirt to celebrate the concept, or you get actual tiles to play with or that use these shapes as especially challenging puzzles. The kind that's extra hard because all the pieces can fit together no matter which ones you use.

Numberphile's Brady Haran did a half hour video interview describing how David Smith and Craig Kaplan developed their geometric solutions, but here's Ayliean's five-and-a-half minute video summarizing it all at warp speed.

And that one-two punch of discovery is the biggest math story of 2023!

Previously on Political Calculations

The Biggest Math Story of the Year is how we've traditionally marked the end of our posting year since 2014. Here are links to our previous editions and our coverage of other math stories during 2022:

• The Biggest Math Story of the Year (2014)
• The Biggest Math Story of 2015
• The Biggest Math Story of 2016
• The Biggest Math Story of 2017
• The Biggest Math Story of 2018
• The Biggest Math Story of 2019
• The Biggest Math Story of 2020
• The Biggest Math Story of 2021
• The Biggest Math Story of 2022
• The Biggest Math Story of 2023
• Whales, Tails and How Far to Trust AI
• Using Math to Boost Your Writing's Readability
• A Formula for Love
• How Much Change Can You Have Without Having Exactly One Dollar in Coins?
• The Maths Hidden Inside St. Paul's Cathedral
• The Geometry of Perfectly Roasted Potatoes
• The One Tile Whose Pattern Never Repeats
• A Game About Love and Graphing
• Patterns of Primes
• The One Aperiodic Monotile to Rule Them All
• The Math That Got Oppenheimer All Worked Up
• There's Always Another Larger Prime Number
• Revisualizing the Map of the Lower 48
• How and When the Three-Point Shot Changed Basketball
• The S&P 500 Reverts Toward the Mean
• The Bias of Coin Tossing
• Games Mathematicians Play

This is Political Calculations' final post for 2023. Thank you visiting us this past year, we hope found the things we wrote either useful, thought-provoking, or entertaining. We'll see you again in the New Year, which we'll kick off with our annual tradition of presenting a tool to help you find out what your paycheck will look like in 2024. Have a wonderful holiday season - we'll only drop in long enough to update this final article of the year with links to other math-related year-end wrap-ups!

Update: Quanta Magazine has put together an article and video with what they consider to be the year's top math stories.

See you next year!

Image credits: Lottery Ticket by Ian Barbour on Flickr. Creative Commons. CC BY-SA 2.0 DEED Attribution-ShareAlike 2.0 Generic. "Cozy office with a green computer screen showing math formulas and diagrams, highly detailed, photorealistic" generated with Stable Diffusion DreamStudio Beta. XKCD: The Value of X. Creative Commons CC BY-NC 2.5 DEED Attribution-NonCommercial 2.5 Generic.